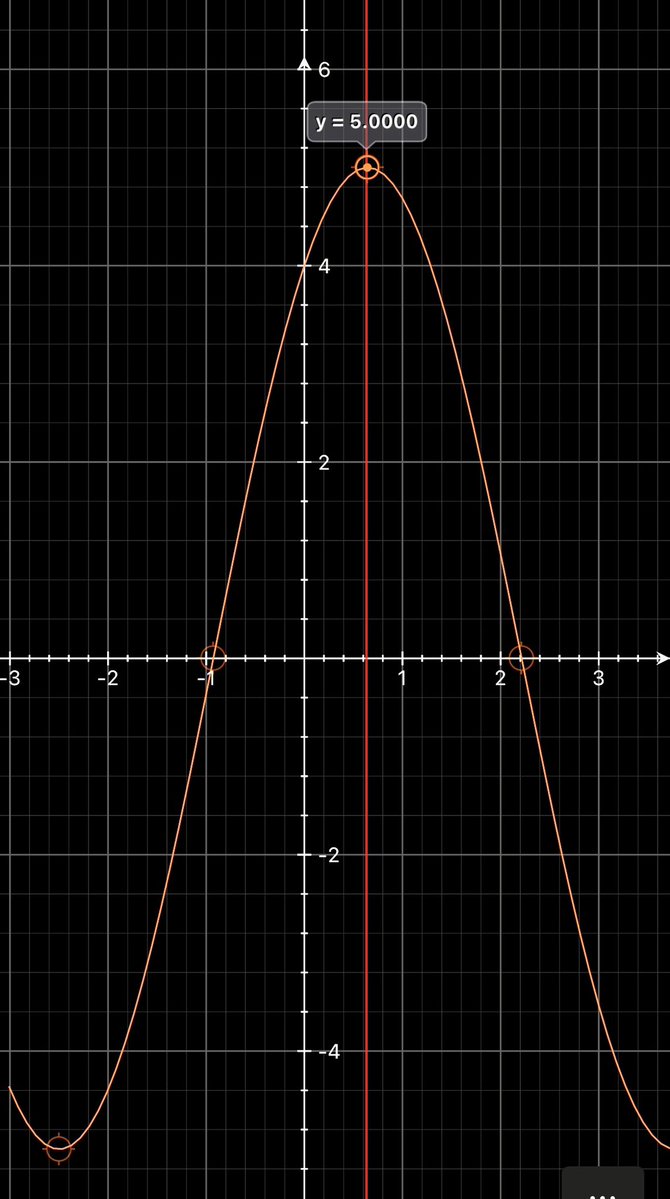
Si: f(x) = 3 cos (x) + 4 sin (x) Con 1ª derivada: f(x) ‘ = 0 f(x) ‘ = - 3 sin (x) + 4 cos (x) Con f(x) ‘ = 0 tan (x) = 4/3 Arctg (4/3) = 0,927295 Sea 2ª derivada: f(x) ‘’ evaluada en “x” f(x) ‘’ = - 3 cos (x) - 4 sin (x) f(0,927295) ‘’ < 0 Luego f(x) = f(0,927295) es Máximo.…
Sea: 🇨🇱🇪🇸 [( x - 1 ) / 3 ] ³ = 64 a = ( x - 1 ) / 3 Luego: a ³ - 64 = 0 a ³ - 4 ³ = (a - 4) (a ² + 4a + 4 ²) = 0 Entonces: a - 4 = 0 a ² + 4a + 4 ² = 0 a1 = 4 a2 = ( - 4 + √(16 - 64)) / 2 a3 = ( - 4 - √(16 - 64)) / 2 Donde: a1 = 4 a2 = - 2 + 2i √3 a3 = - 2 - 2i √3…
( x + 2 ) ² = 49 ( x + 2 ) ² - 7 ² = 0 ( x - 5 ) ( x + 9 ) = 0 x1 = 5 x2 = - 9
45 / 3 = 15 39 / 3 = 13 X / 3 = 11 Then x = 33
Easy Sin ² (x) + Sin ² (90 - x) = 1 Then Sin ² (1) + Sin ² (89) = 1 Sin ² (2) + Sin ² (88) = 1 Sin ² (3) + Sin ² (87) = 1 . . . Sin ² (44) + Sin ² (46) = 1 And Sin ² (45) = 1/2 Sin ² (90) = 1 Then 44 ∑ Sin²(x)+Sin²(90-x) + 1 + 1/2 1 = 44 + 1 + 1/2 Addition = 45.5 q.e.d
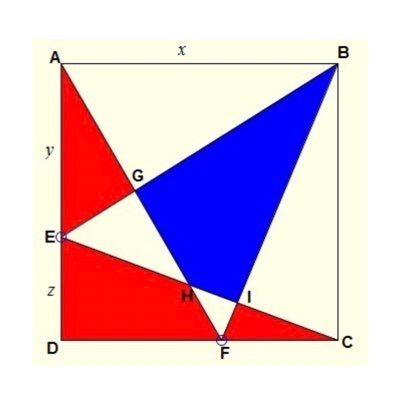
Si diagonal = √180 = 2√45 Si diagonal = > a √2 = 2√45 a = √90 = 3 √10 Área = a ² / 2 = 45 Área = 45 cm ²
1/9 + 1/18 + 1/30 + 1/45 + 1/63 + … oo ∑ = 1/3

By Pythagoras: A: √ 45 B: √ 50 C: √ 52 D: √ 40 C > B > A > D Finally C is the largest.
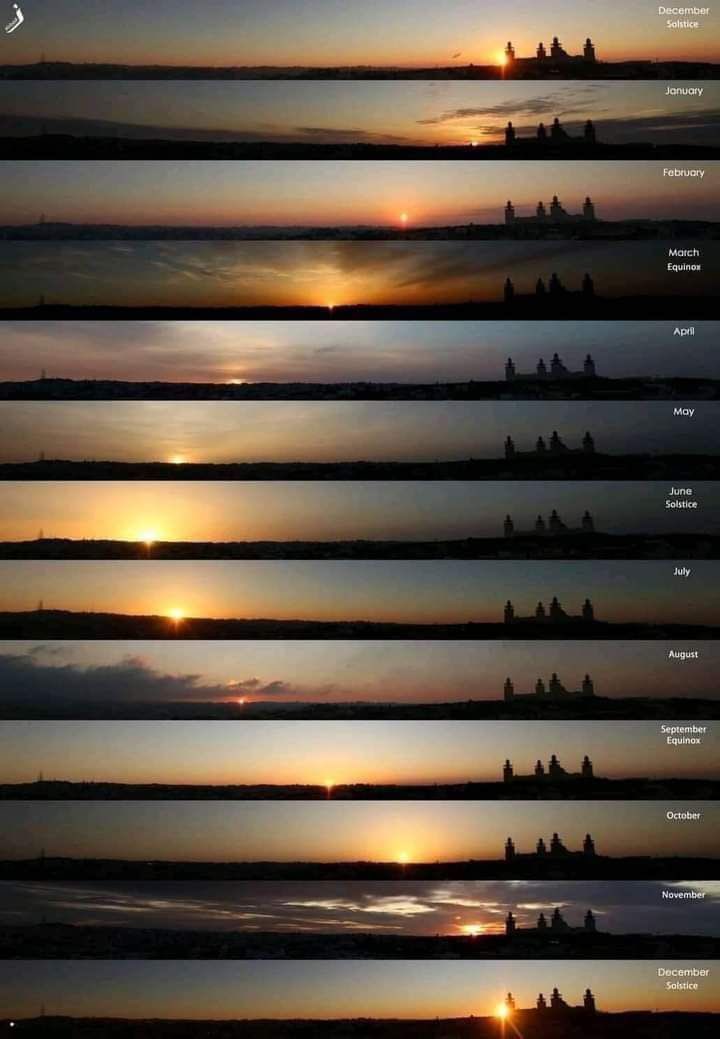
TRIGONOMETRÍA Y NATURALEZA 12 fotos del Sol en doce meses, el mismo día, el mismo lugar y a la misma hora. La misma cámara, la misma exposición, misma ASA, mismo teleobjetivo y mismo enfoque. Una sinusoide perfecta.

cos x - sin x = 1 /( ) ² cos ²x - 2sin x cos x + sin ²x = 1 If: cos ²x + sin ²x = 1 Then: sin x cos x = 0 x1 = 0º + 2 π n ∀ ∈ |R or x2 = π/2 + 2 π n ∀ ∈ |R where: i) sin x = 0 ∧ cos x = 1 or ii) sin x = 1 ∧ cos x = 0 Then: (cos x)^2022 + (sin x)^2022 = 1
🇪🇸 Suponga que: (x + 3)(x + 5)(x + 7)(x + 9) = 9 Dado que 3,5,7,9 son impares consecutivos, se considera el promedio de los términos libres: (3 + 5 + 7 + 9) /4 = 24/4 = 6 Luego: x = - 6 es solución factible. Combinaciones que dan 9 ( -3 )( -1 )( 1 )( 3 ) = 9 Luego: Si x + 3…
Sea: Volumen x = Volumen y = 1.000 L X con altura hx Y con altura hy Asumiendo el mismo líquido en ambos recipientes y ambos sujetos a sólo la acción de la gravedad se tiene que: La velocidad de salida del líquido es: Vx = √(2ghx) Vy = √(2ghy) Luego el caudal Q es: Qx = Vx…
Let the Algebraic Method be: y = 2^x + x - 5 If: a = 2^x ln a = x ln 2 a = e ^ (x ln 2) 2^x = e ^ (x ln 2) By Taylor Series: e^x = 1 + x + x ² / 2! + x ³ / 3! + …. If we replace: 2^x = 1 + (x ln 2) + (x ln 2) ²/2! + (x ln 2) ³/3! +…. If we expand to degree 3. Then: 2^x +…
1 ² + 2 ² = 5 1 + 4 = 5 1 ² + 2 ² + 3 ² + 4 ² + 5 ² = 55 1 + 4 + 9 + 16 + 25 = 55
Favorable Cases = ( 6 * 5 * 4 ) * 3 = 360 Possible Cases = 3 * 6 ³ = 648 Probability = 360 / 648 = 5/9 Probability = 0,55555 = 55,555 %
x ² - x ³ = 80 x ² - x ³ - 80 = 0 (x + 4) (x ² - 5x + 20) = 0 Se cumple que: x + 4 = 0 x ² - 5x + 20 = 0 Luego: x1 = - 4 x2 = (5 + i √ 55) / 2 x3 = (5 - i √ 55) / 2
DATO FREAK. El mayor número primo descubierto al día de hoy es: ________________________________ | | | M = 2 ¹³⁶ ²⁷⁹ ⁸⁴¹ - 1 | | ¹³⁶ ²⁷⁹ ⁸⁴¹…
Un 18 de Agosto de 1685 nace Brook Taylor, un matemático británico, autor del teorema que lleva su nombre y de destacadas contribuciones al desarrollo del cálculo diferencial. Las series de Taylor son un desarrollo que transforma una función derivable en una serie infinita.


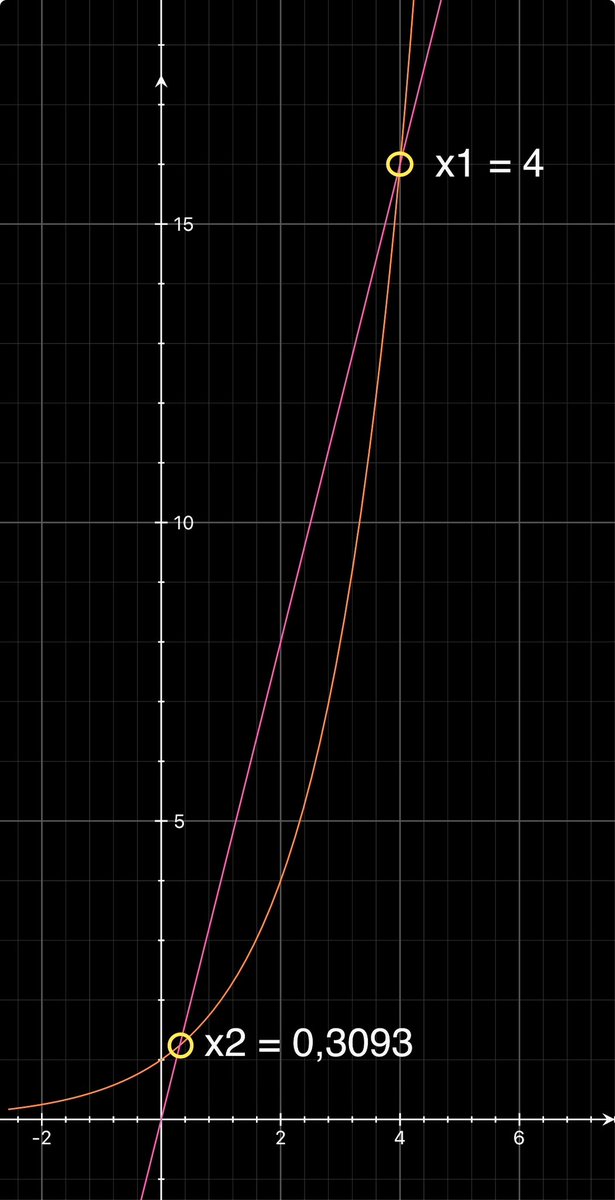
Si 2^x = 4x Sean x1 = 4 X2 = ? Con 2^x = e^(x ln2) Por Taylor ∀ z < 1 e^z = 1 + z + z ²/2! + … Si z => x ln2 e^(x ln2) = 1+ xln2+ (xln2) ²/2 = 4x Ec de 2º grado A= (ln2)²/2 = 0,24022 B= (ln2)-4 = -3,30685 C= 1 Con x2 < 1 x2 = (3,30685 - 3,15821) / 0,48044 x2 = 0,3093 Aprox.
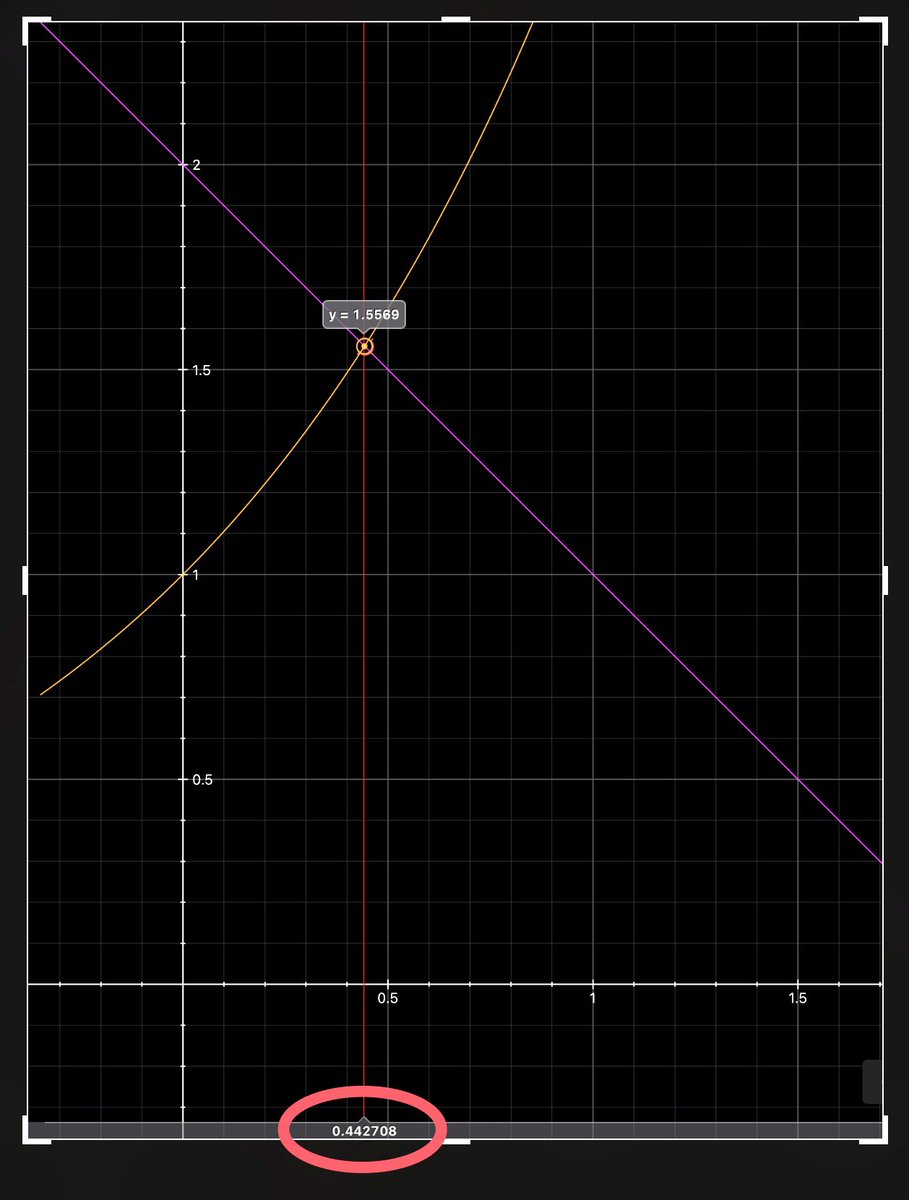
be x + e^x = 2 e^x = 2 - x By Taylor: e^x = 1 + x + x ²/ 2! + x ³/ 3! +… Next, let's consider even the quadratic term. 2 - x = 1 + x + x² / 2! so x² + 4x - 2 = 0 We consider the positive root x > 0 x = ((2 √6) - 4) / 2 x ≈ 0.44 Approximate root.
United States 趨勢
- 1. Liverpool 156K posts
- 2. #UFCQatar 24.4K posts
- 3. Mizzou 3,186 posts
- 4. Slot 111K posts
- 5. Luke Riley 1,888 posts
- 6. Mateer 1,297 posts
- 7. Chris Paul 11.3K posts
- 8. Rutgers 4,637 posts
- 9. Arbuckle N/A
- 10. Newcastle 33.3K posts
- 11. Missouri 9,314 posts
- 12. Lamine 49.4K posts
- 13. #Sooners N/A
- 14. Dalby 1,475 posts
- 15. Anfield 29.3K posts
- 16. Isak 30.5K posts
- 17. #kufball N/A
- 18. Klopp 10.1K posts
- 19. Forest 122K posts
- 20. Reggie Evans N/A
Something went wrong.
Something went wrong.