Differential Eqns
@diff_eq
Tweets on ordinary and partial differential equations from @JohnDCook
You might like
One reason fractional differential equations can be useful is that fractional derivatives contain non-local information.
Differential equations in the complex plane johndcook.com/blog/2023/07/0…
If f(x + iy) = u(x,y) + i v(x, y) is analytic, then u and v are harmonic, i.e. u_xx + u_yy = 0 and v_xx + v_yy = 0.
If f(x + iy) = u(x,y) + i v(x, y) is analytic, then u and v satisfy the Cauchy-Riemann equations: u_x = v_y, v_x = -u_y.
Estimating local error with Runge-Kutta-Fehlberg, a.k.a. RKF45 johndcook.com/blog/2020/02/1…
Robin boundary conditions specify a linear combination of solution and normal derivative values on the boundary.
'The fact is that PDEs, in particular those that are nonlinear, are too subtle to fit into a too general scheme. On the contrary, each important PDE seems to be a world in itself.' -- Sergiu Klainerman
Stabilizing the Spherical Pendulum from Scratch community.wolfram.com/groups/-/m/t/3…
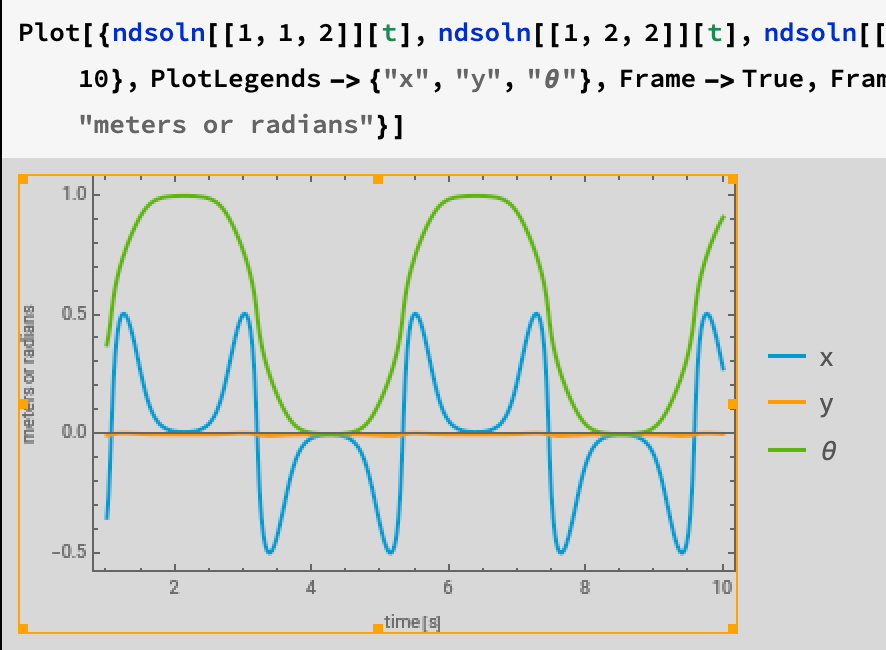
Third-order ODEs are uncommon, and usually nonlinear, such as the Blasius equation. kitchingroup.cheme.cmu.edu/blog/2013/03/1…
Bernoulli's equation: y' + p(x) y = q(x) y^n. Can be turned into a linear equation by the substitution u = y^(1-n).
Dirichlet boundary conditions specify solution values on boundary. Neumann boundary conditions specify normal derivatives of solution.
There are important non-linear PDEs with closed-form solutions johndcook.com/blog/2024/04/2…
“Good theory is (almost) as useful as exact formulas.” — Lawrence Evans re PDEs
Conservative vector fields and exact ODEs johndcook.com/blog/2022/12/0…
A solution corresponding to an eigenvalue with positive real part grows exponentially.
If a linear ODE has complex eigenvalues, solutions oscillate. If real parts are negative, oscillations decay exponentially.
United States Trends
- 1. Penn State 18.7K posts
- 2. #twitchrecap 12.3K posts
- 3. #TADCFriend 1,547 posts
- 4. Romero 22.2K posts
- 5. Slay 19.7K posts
- 6. Pat Kraft 2,180 posts
- 7. Paul Dano 1,115 posts
- 8. Zion 9,544 posts
- 9. #GivingTuesday 31.5K posts
- 10. Fulham 44.9K posts
- 11. Lewandowski 27.7K posts
- 12. Larry 61.7K posts
- 13. Tarantino 7,586 posts
- 14. Sabrina Carpenter 42.7K posts
- 15. Adam Thielen 3,983 posts
- 16. Alek Manoah N/A
- 17. Pedri 58.4K posts
- 18. Franklin 66.5K posts
- 19. Rashford 10.7K posts
- 20. Blanca 30.3K posts
You might like
-
Algebra Etc.
@AlgebraFact -
Analysis Fact
@AnalysisFact -
Probability Fact
@ProbFact -
Topology Fact
@TopologyFact -
Network Fact
@NetworkFact -
Data Science Fact
@DataSciFact -
Logic & Applications
@LogicPractice -
Grant Sanderson
@3blue1brown -
Computer Science
@CompSciFact -
Science and Medicine
@ScienceTip -
Scientific Python
@SciPyTip -
Maths History
@mathshistory -
Signal Processing
@DSP_fact -
Functor Fact
@FunctorFact -
TeX and Typography
@TeXtip
Something went wrong.
Something went wrong.