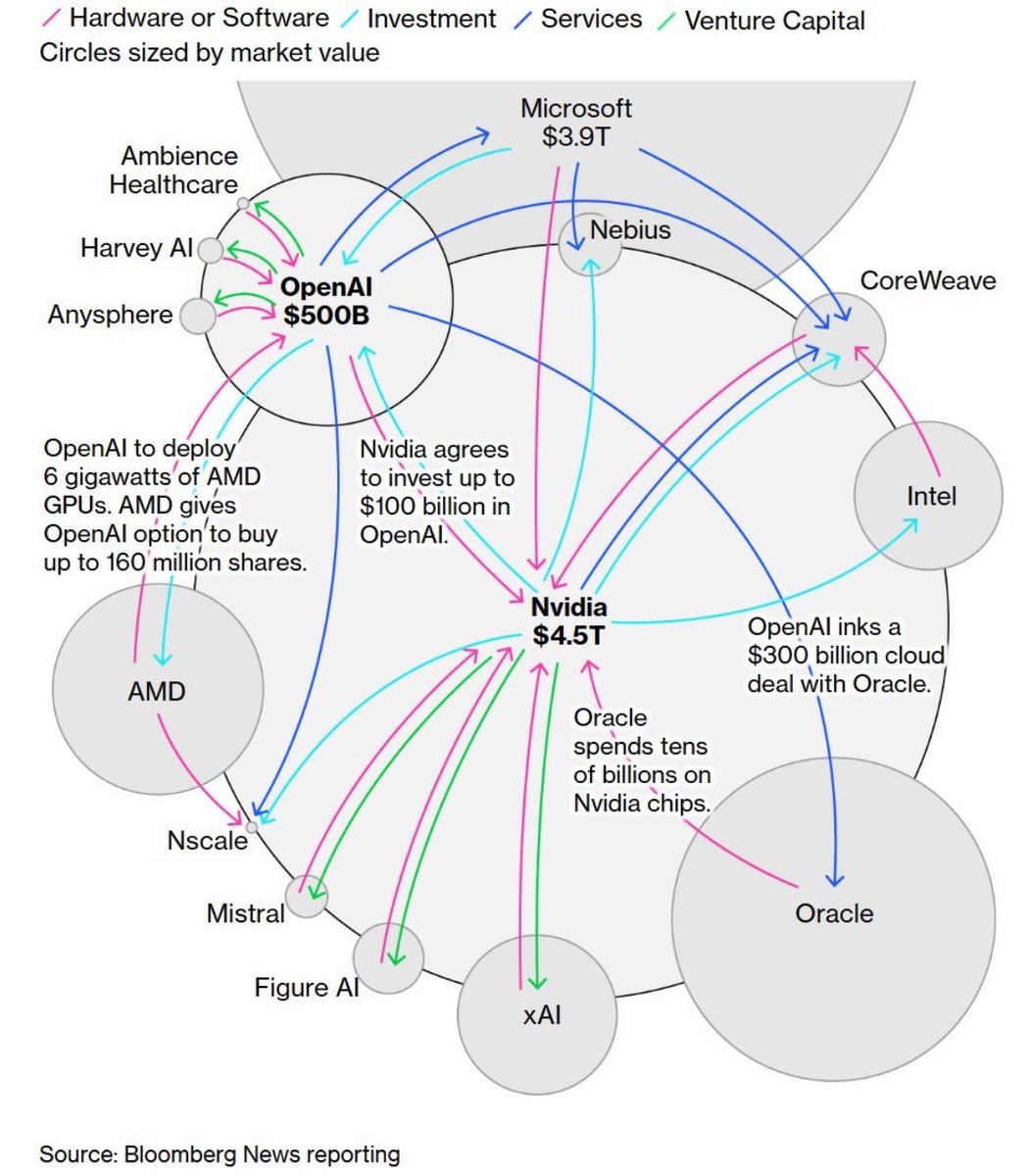
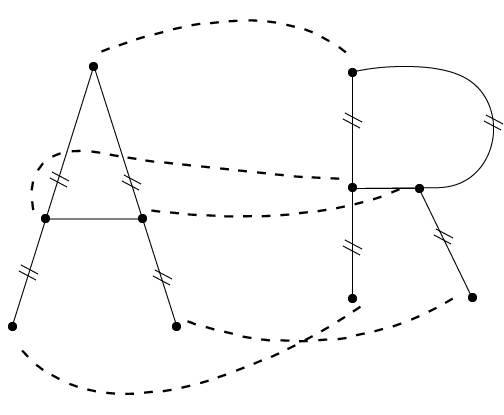
#homeomorphic_graphs 搜尋結果
DMS-Isomorphic Graphs Consider a graph G(V, E) and G* (V*, E*) are said to be isomorphic if there exists one to one correspondence i.e. bit.ly/Isomorphic_Gra… #Isomorphic_Graphs #Homeomorphic_Graphs #Subgraph
This is the start of homology! We're embedding elementary manifolds (lines, triangles, tetrahedra, etc.) and looking at their boundaries! Specifically at how their boundaries "cancel" or don't If I were your teacher, I would now guide you through a series of examples where
How do you prove that the circle and the line are not homeomorphic? Well, if you work really hard you can show that one is contractible and the other is not (exercise) But like: just look at them! They're obviously different! The circle has a "hole" while the line doesn't
せっかくだから、Mathematicaでpersistent homologyを勉強する。 persistent homologyについては Introduction to Persistent Homology for Graph Analysis (PDF)が分かりやすい www2.math.kyushu-u.ac.jp/~skaji/slides/…
Homotopy invariance ensures properties remain constant under continuous deformation (stretching or bending). In machine learning, this powers Topological Data Analysis (TDA), allowing models to extract robust features from noisy data—recognizing that a distorted handwritten digit…
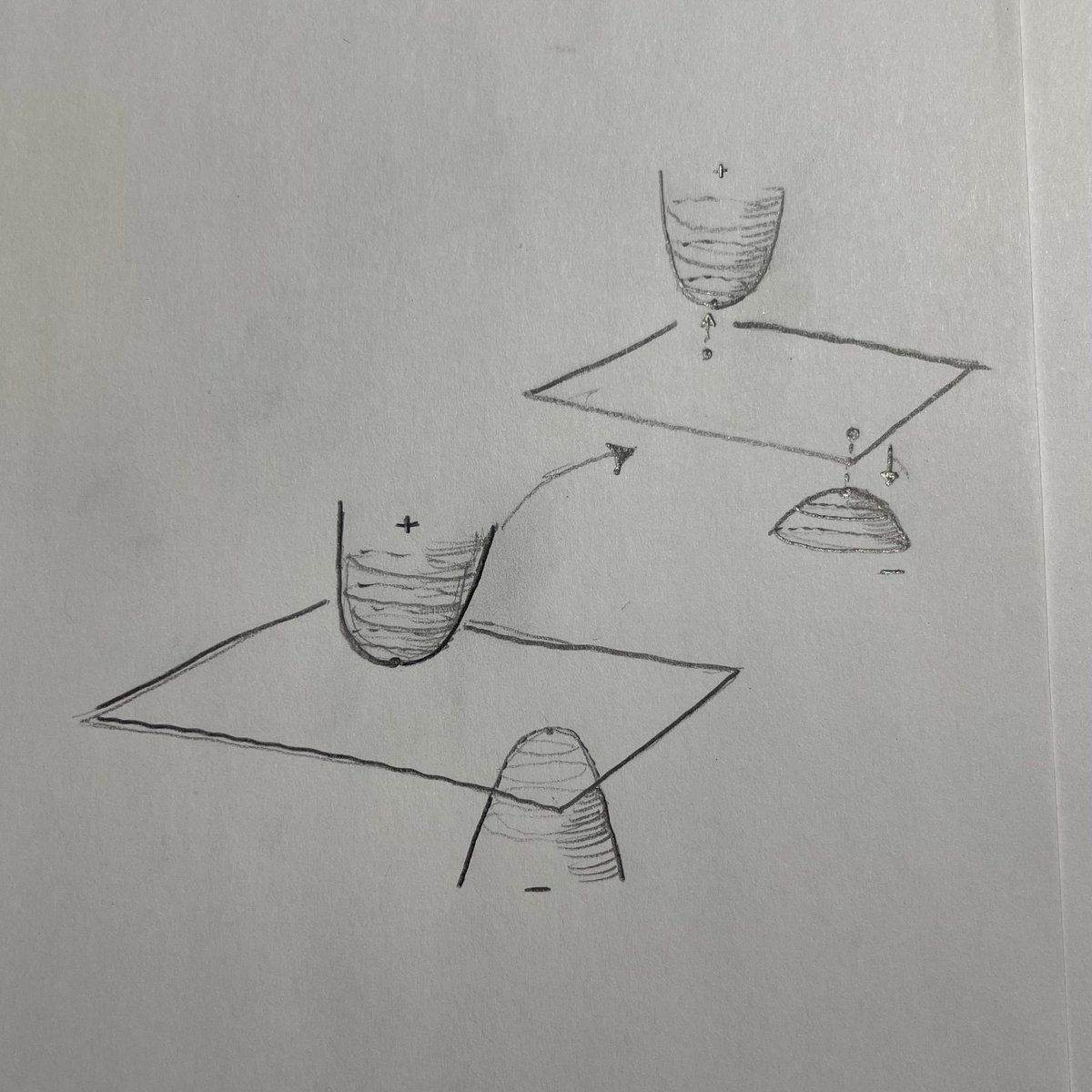
The graph of 𝘧 in ℝ³ is a connected 2d-surface homeomorphic to ℝ². The roots of 𝘧 are points of the surface touching the 0-plane. One can nudge the areas around the roots up or down to separate this connected surface into +& - pieces … v —— (intuitive approach) ^
Inti Cruz Diaz: A classification of pseudo-Anosov homeomorphisms I: the geomet... arxiv.org/abs/2511.19774 arxiv.org/pdf/2511.19774 arxiv.org/html/2511.19774
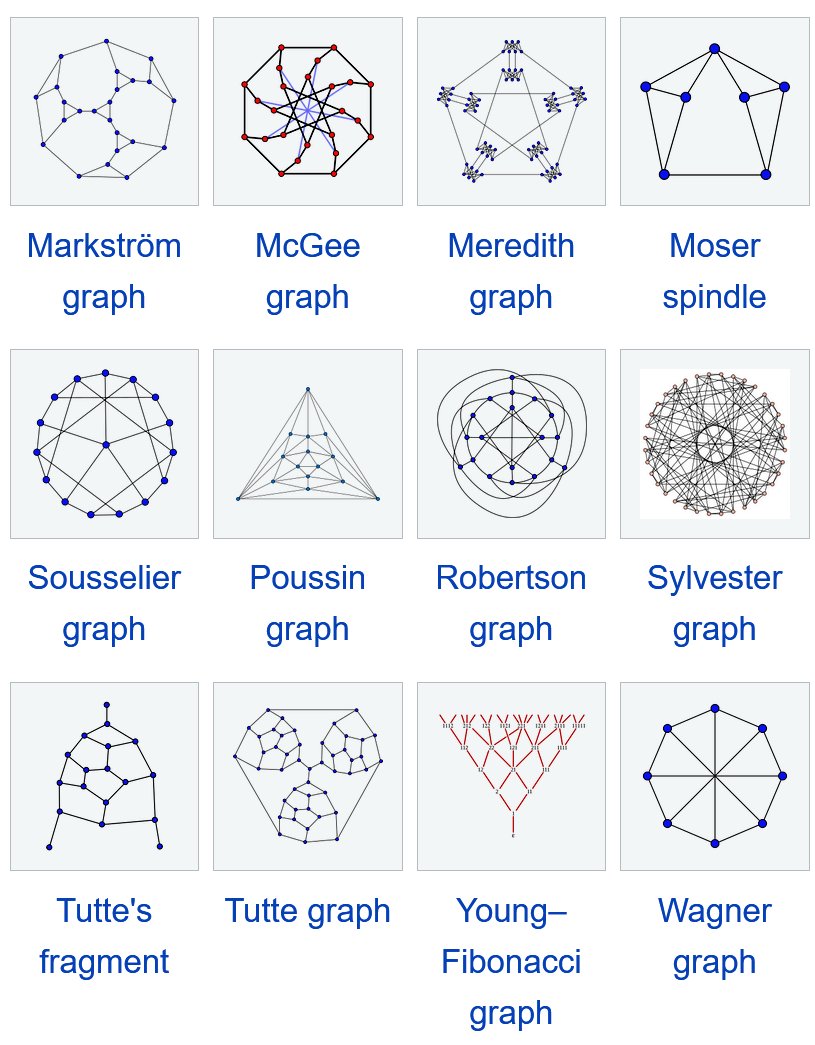
Math. Symphony of Symmetry: 12 More Masterpieces of Graph Theory. Gallery of "named graphs": Markström graph, McGee graph, Meredith graph, Moser spindle, Sousselier graph, Poussin graph, Robertson graph, Sylvester graph, Tutte's fragment, Tutte graph, Young–Fibonacci graph,…
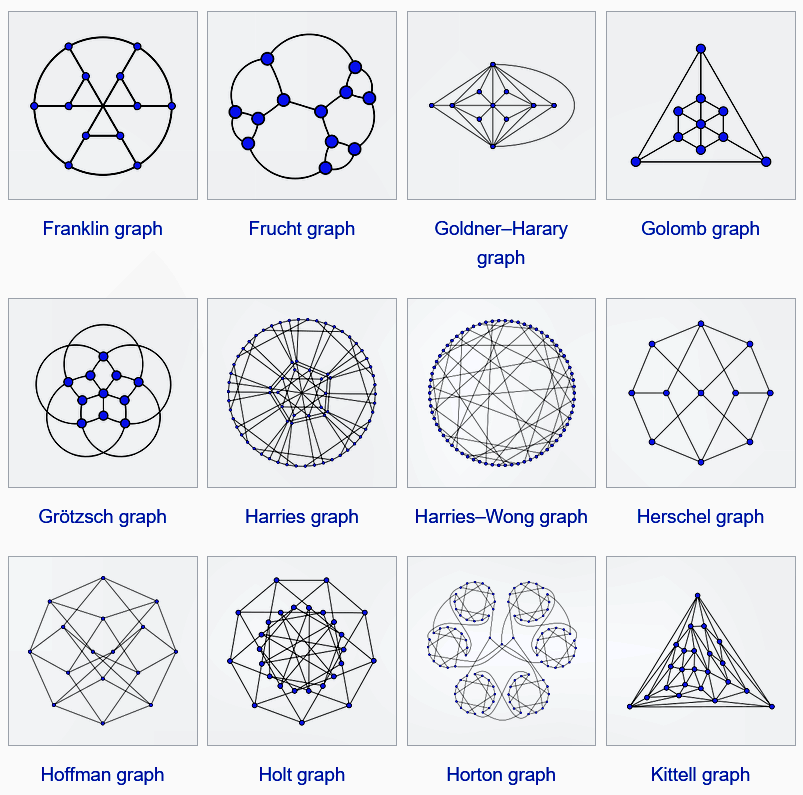
Math. Symphony of Symmetry: 12 More Masterpieces of Graph Theory. Gallery of "named graphs": Franklin graph, Frucht graph, Goldner–Harary graph, Golomb graph, Grötzsch graph, Harries graph, Harries–Wong graph, Herschel graph, Hoffman graph, Holt graph, Horton graph, Kittell…
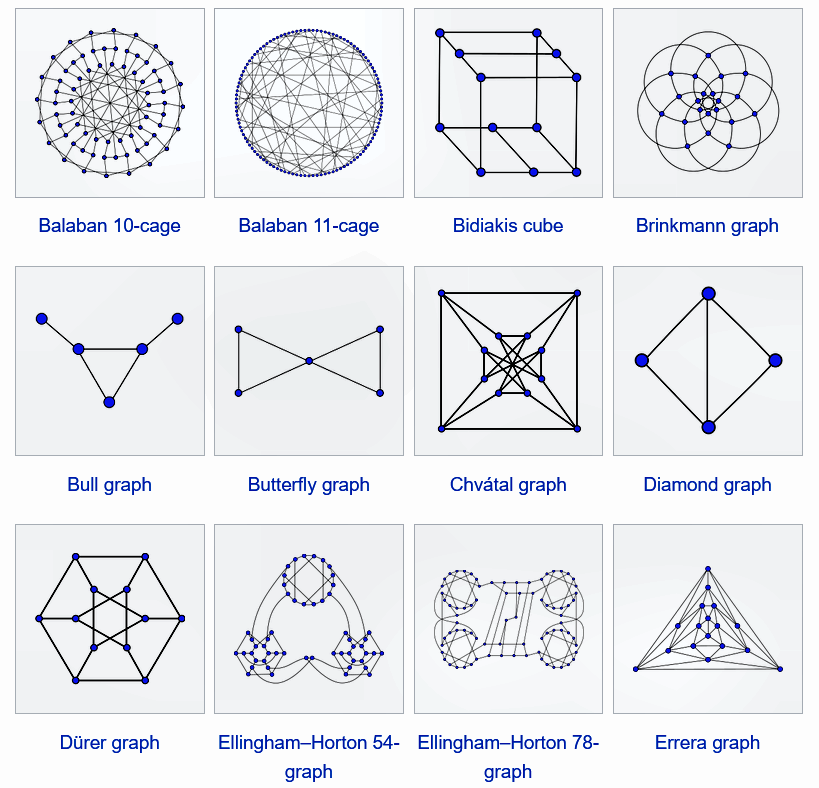
Math. Symphony of Symmetry: 12 Masterpieces of Graph Theory. Gallery of "named graphs": Balaban 10-cage, Balaban 11-cage, Bidiakis cube, Brinkmann graph, Bull graph, Butterfly graph, Chvátal graph, Diamond graph, Dürer graph, Ellingham–Horton 54-graph, Ellingham–Horton 78-graph,…
Give your class this chart. Then maybe your teacher will make time to teach you something valuable.

A graph is nonplanar if and only if it contains a subgraph that is homeomorphic to K5 or K3,3
Does anyone have any random fun facts about a very niche subject. I'm bored and love learning random things
Homology is a fundamental concept in algebraic topology. It allows you to quantify how many holes a space has. When I first learned it, however, it was very mystifying. It took me years to understand the intuitions behind it. In this thread, I wanted to share this intuition at…
A topological space of fonts 🔤 Do you see the separation of serif and non-serif fonts? bit.ly/3dDMb67 (Neill D.F. Campbell and Jan Kautz, SIGGRAPH 2014) #math #science #iteachmath #mtbos #visualization #elearning #topology
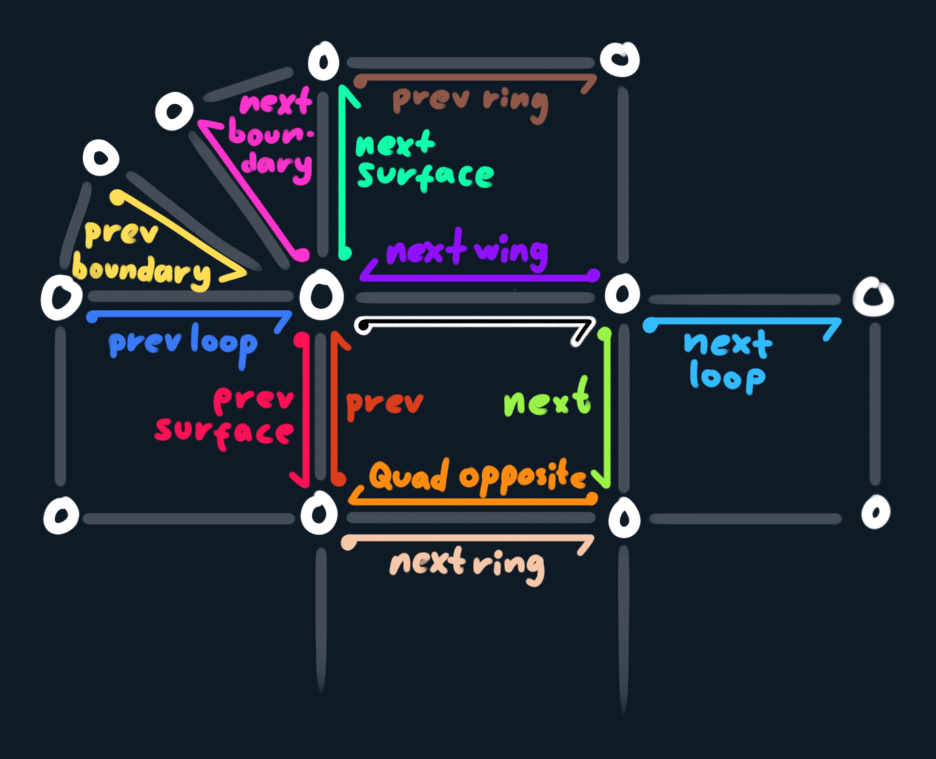
this has become my most used reference in the notes for my 3D editor it's a diagram with names of all topology traversal functions I've got - all relative to the black half edge with a white outline in the middle
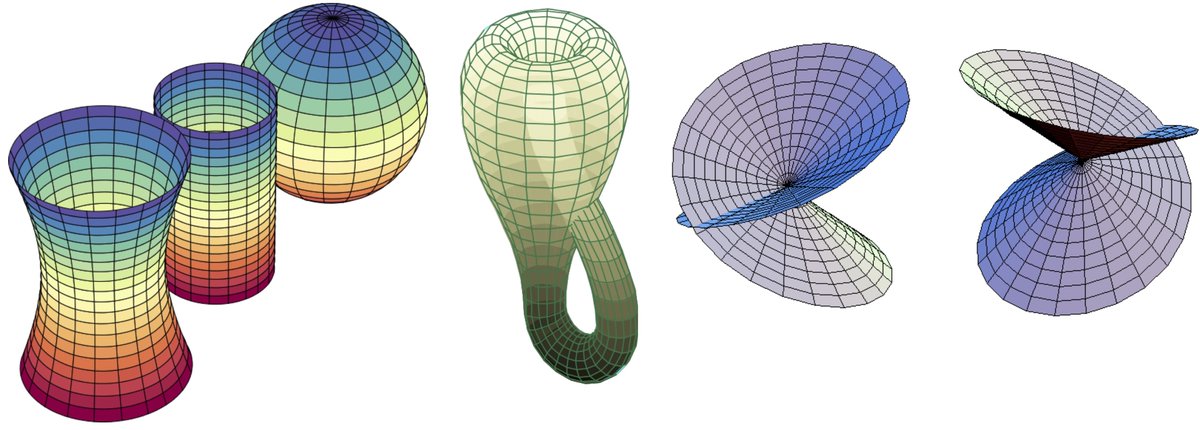
More formally, each point has a neighbourhood that is homeomorphic to Euclidean space. For example, the Earth appears to be locally flat, but is in fact round!

Natural graphs don't look like hairballs if you stratify them by node degree during layout. They look like beautiful mountains 🏔️😍 Here is an ego graph, where each node is bound to Z=deg(node) plane
This figure summarizes the landscape of topological neural network architectures on hypergraphs, simplicial, cellular, & combinatorial complexes in a unified graphical notation. Check out our paper and full repository of TNN equations for more ✨

Topological Deep Learning is an immensely powerful and fast emerging field. Our new literature review arxiv.org/abs/2304.10031 is out and here’s why I’m very excited about it🧵1/5
Yet another excellent book to get an introduction to topological data analysis. Homology, Morse theory en.wikipedia.org/wiki/Topologic… cambridge.org/core/books/top…

DMS-Isomorphic Graphs Consider a graph G(V, E) and G* (V*, E*) are said to be isomorphic if there exists one to one correspondence i.e. bit.ly/Isomorphic_Gra… #Isomorphic_Graphs #Homeomorphic_Graphs #Subgraph

Something went wrong.
Something went wrong.
United States Trends
- 1. #GivingTuesday 18.6K posts
- 2. #twitchrecap 3,279 posts
- 3. Costco 43.4K posts
- 4. #csm222 3,715 posts
- 5. Susan Dell 4,015 posts
- 6. #AppleMusicReplay 6,074 posts
- 7. Lucario 19K posts
- 8. Michael and Susan 2,738 posts
- 9. NextNRG Inc. 2,014 posts
- 10. #NXXT_NEWS N/A
- 11. Trump Accounts 10.3K posts
- 12. King Von 1,330 posts
- 13. Good Tuesday 43K posts
- 14. Pentagon 73.9K posts
- 15. Hoss Cartwright N/A
- 16. Isack 25.6K posts
- 17. Gallo 10K posts
- 18. Tiki 2,817 posts
- 19. Dart 44.9K posts
- 20. $AMZN 11.1K posts