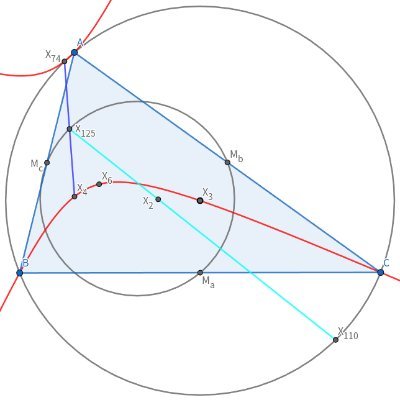
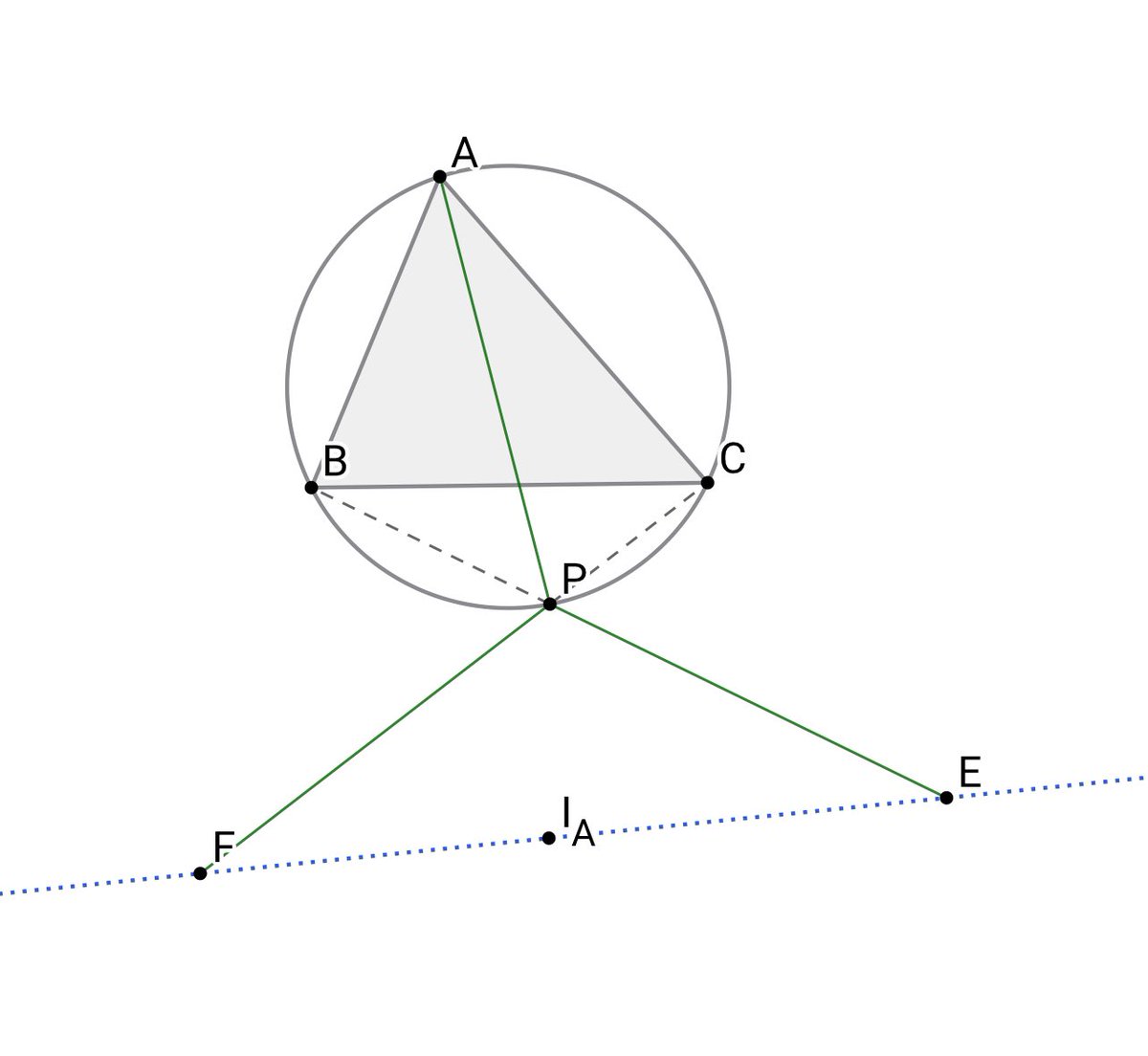
三角形ABCと弧BC上の点Pについて,半直線BP,CP上にそれぞれ点E,FをAP=PE=PFを満たすようにとる.このとき,Pに依らず直線EFは常にある定点(= A-傍心)を通る.
三角形ABCについて,その内心をI,外心をOとする.直線AIが円ABCと再び交わる点をVとし,OIの中点をSとしたとき,AIの垂直二等分線,OVの垂直二等分線及びSを通りVSに垂直な直線は一点で交わる.

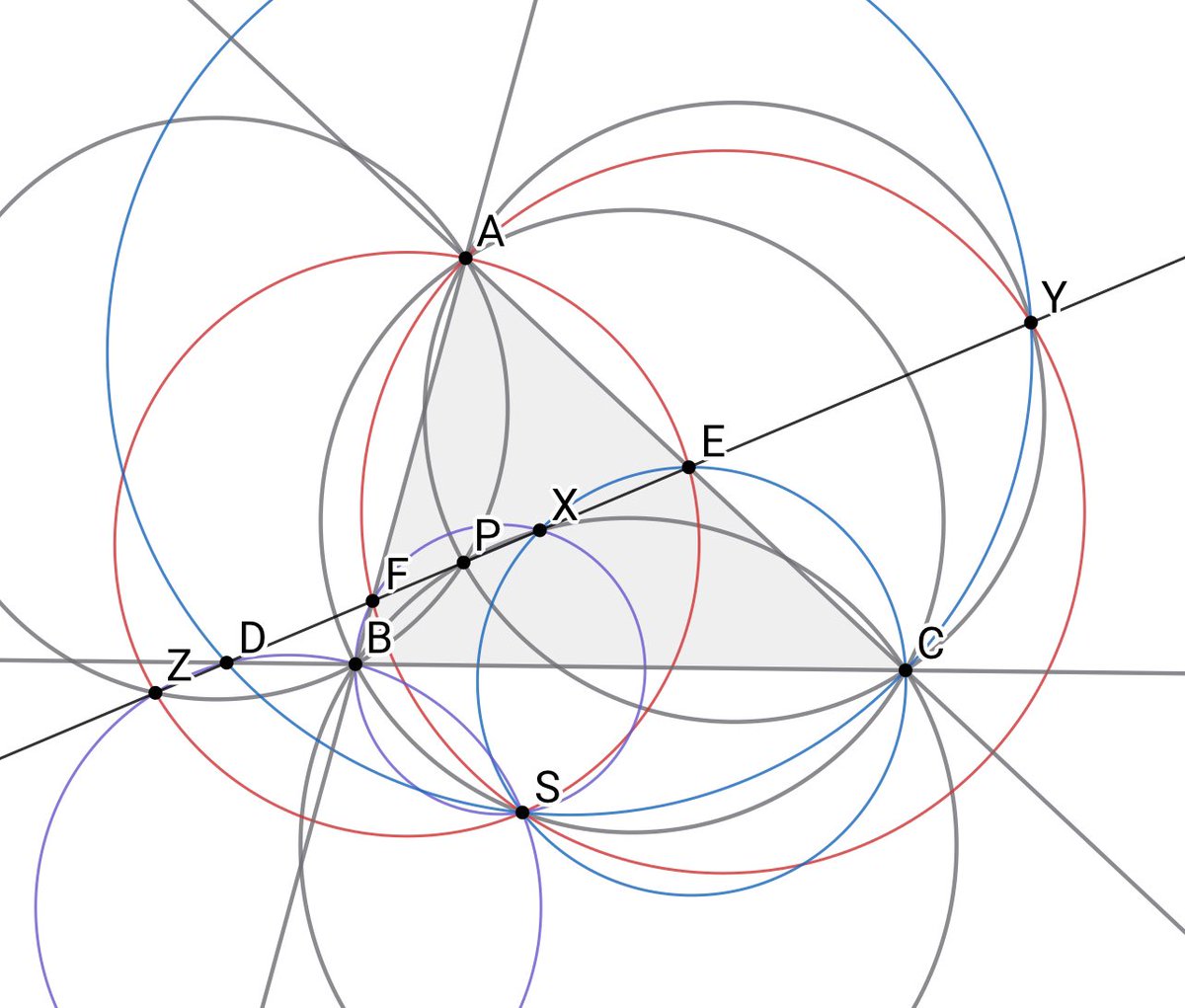
三角形ABCとPについて,Pを通る直線が直線BC,CA,AB及び円PBC,PCA,PABと交わる点をそれぞれD,E,F,X,Y,Zとする.このとき,7円ABC,AEZ,AFY,BFX,BDZ,CDY,CEXは共点である.
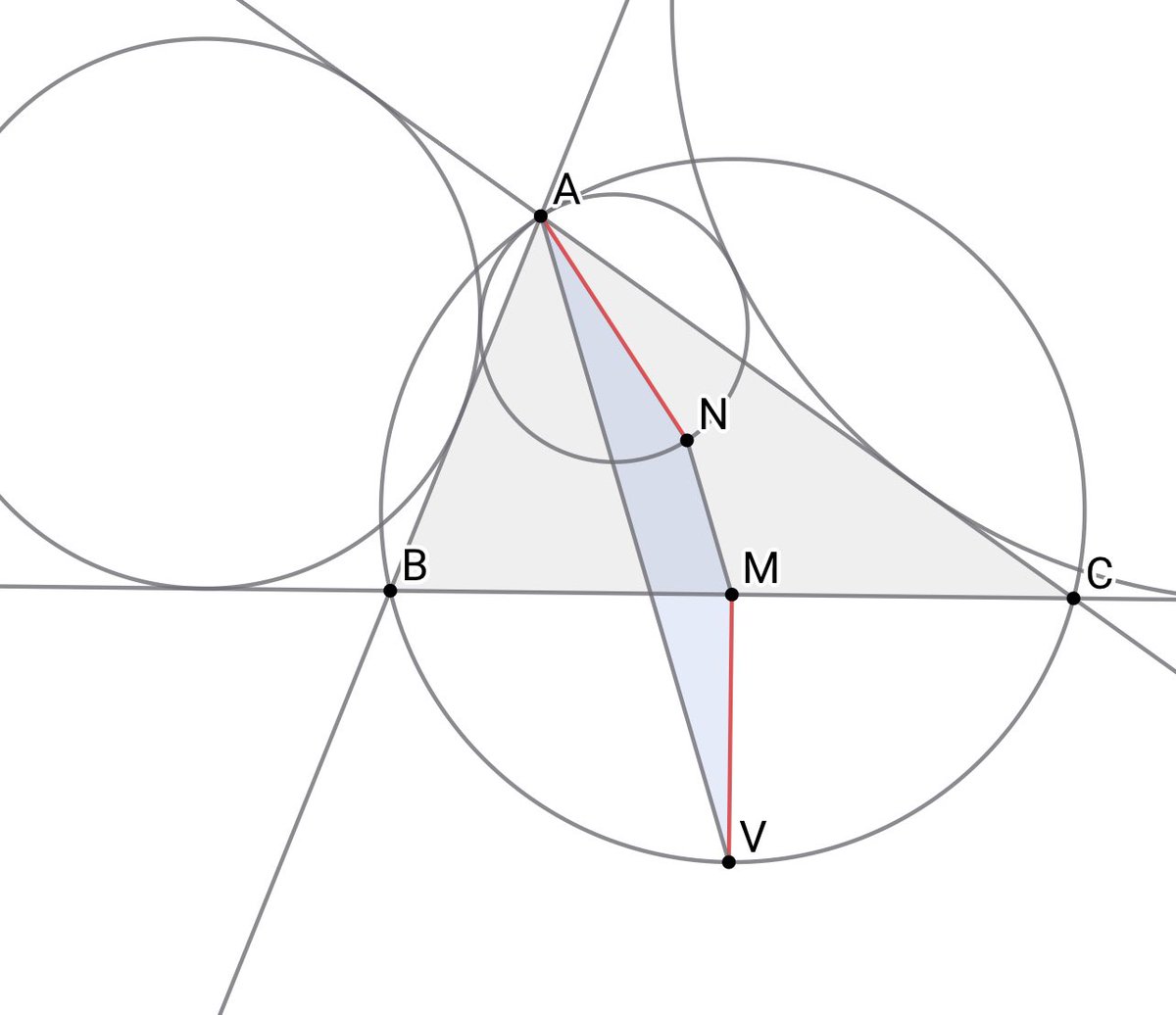
三角形ABCについて,BCの中点をMとし,弧BC(Aを含まない)の中点をVとする.四角形ANMVが等脚台形となるように点Nを取ったとき,ANを直径とする円は円ABC, B-傍接円, C-傍接円に接する.
三角形ABCについて,その外心をOとし,任意の点Pの垂足三角形をΔとする.このとき,Δの面積はPOの長さにのみ依存する.(Simsonの定理の拡張)
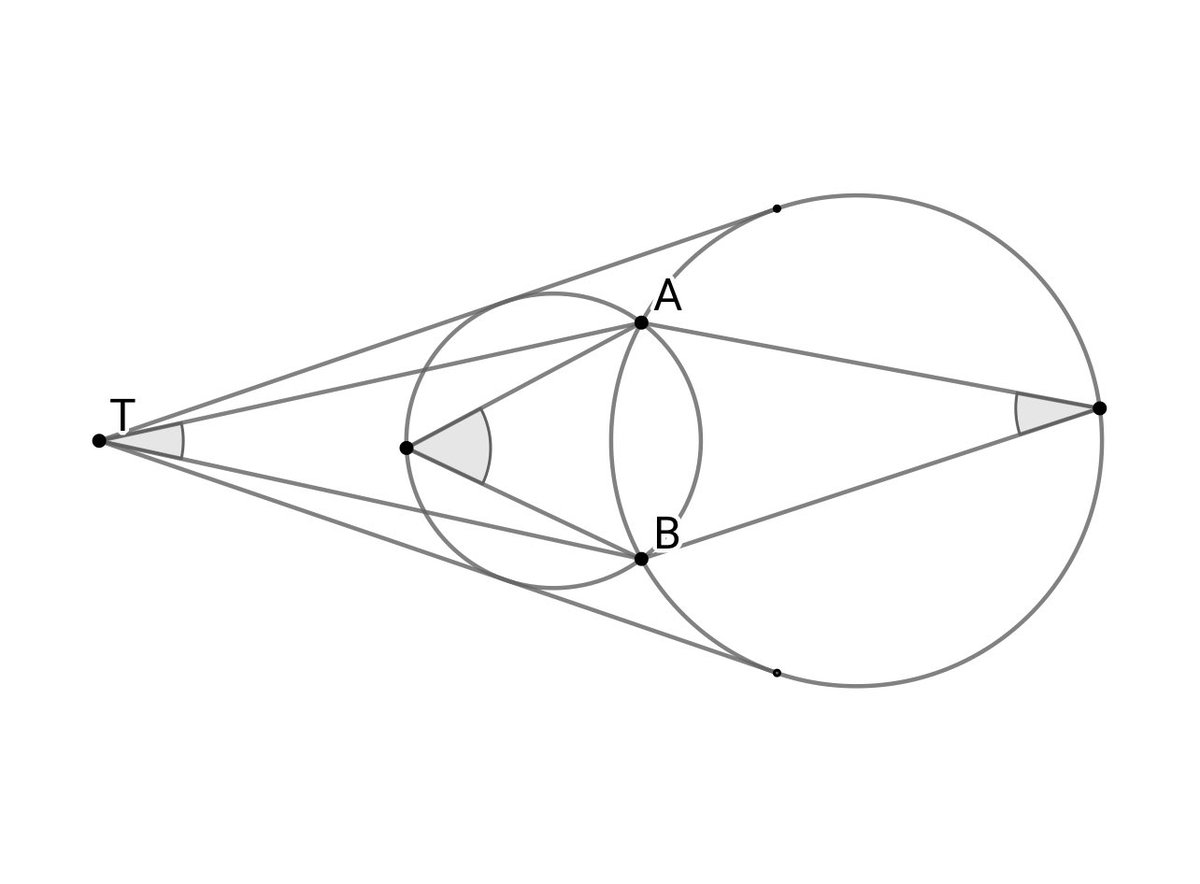
2円ω1,ω2 (ω1<ω2)が2点A,Bで交わっており,さらに共通外接線はTで交わっている.このとき,∠ATBはω1におけるABの円周角とω2におけるABの円周角の差に等しい.
三角形ABCと点K,L,Pについて,K,Lのチェバ三角形をそれぞれA_0B_0C_0,DEFとし,直線PA_0,PB_0,PC_0が円PBC,PCA,PABと再び交わる点をそれぞれA_1,B_1,C_1とする.直線A_1D,B_1E,C_1Fが円PBC,PCA,PABと再び交わる点をそれぞれX,Y,Zとしたとき,4点P,X,Y,Zは共円.

United States الاتجاهات
- 1. #AcousticPianoSnowGlobe 1,688 posts
- 2. Cheney 26K posts
- 3. Nano Banana Pro 10.6K posts
- 4. #TSTheErasTour 1,422 posts
- 5. #NXXT_NEWS N/A
- 6. FINAL DRAFT FINAL LOVE 239K posts
- 7. #LoveDesignFinalEP 220K posts
- 8. YOYOK N/A
- 9. Nnamdi Kanu 145K posts
- 10. #TheGamingAwards N/A
- 11. Husqvarna N/A
- 12. Haymitch 13.6K posts
- 13. First Take 42.5K posts
- 14. SEDITIOUS BEHAVIOR 5,733 posts
- 15. sohee 39.9K posts
- 16. Happy Birthday Erika 3,863 posts
- 17. Trump and Vance 24.3K posts
- 18. Pablo 65.6K posts
- 19. Unemployment 30.6K posts
- 20. Good Thursday 39.4K posts
Something went wrong.
Something went wrong.