Algorithmic Puzzles
@algopuzzles
Problems in graph theory, combinatorics and algorithms. Contests are held on Algo Muse website.
Talvez você curta
Prove that any convex polygon of area 1 sq. unit can be covered with a rectangle of area 2 sq. units.
Let S be a subset of [n]:={1,2,...,n} such that no three numbers in S are in arithmetic progression. Prove that |S| < 0.98n, using only elementary arguments.
Show that a map formed on a plane by finitely many circles is 2-colourable.
Prove that a graph with n nodes either has a path of length k or has O(kn) edges.
Consider the set of n vertices of a convex polygon. Count the number of non-crossing paths that visit all the vertices. [Src: 11011110, David Eppstein] #exportober
![algopuzzles's tweet image. Consider the set of n vertices of a convex polygon. Count the number of non-crossing paths that visit all the vertices. [Src: 11011110, David Eppstein]
#exportober](https://pbs.twimg.com/media/Ffwu2BRaMAIKUpV.png)
You are given an array A[1..n] in which each element is at most k positions away from the position it would have been in if A was sorted. You don't know the value of k. Design an algorithm to sort the array in O(n log k) time. #exportober
![algopuzzles's tweet image. A tiling problem with wireframes. [Source: Micheal Brand]. #exportober](https://pbs.twimg.com/media/Fee1KKWakAAlhcs.png)
Consider the following variant of chess: In the first move only, white can opt in to make a single chess move or two consecutive chess moves; after that it is usual chess. Let's call this variant mhess. Theorem: In mhess, white can always force at least a draw.
Take an nxn grid. Colour each square white or black in such a way that each 2x2 grid has exactly 2 white and 2 black squares. How many ways can this be done? Like I said, it is accessible to high school students and teachers. Of course counting options one by one is suicidal.
Tricky math puzzle: Suppose we have a disk of diameter 20 and strips of width 1 and length 20. We can cover the disk using 20 strips by laying them side-by-side. Can we do it with 19? No cutting is allowed. My next tweet is the answer/solution. 1/6
Suppose A is the adjacency matrix of an undirected graph. Prove that the absolute value of any eigenvalue of A is less than the max. degree of the graph. #exportober
On an nxn grid a few nodes are set on fire at t=0. The fire spreads like this: if at least two neighboring nodes of node x are lit, then node x will also catch fire in the next time step. What's the minimum number of nodes that have to be lit to burn the entire grid? #exportober
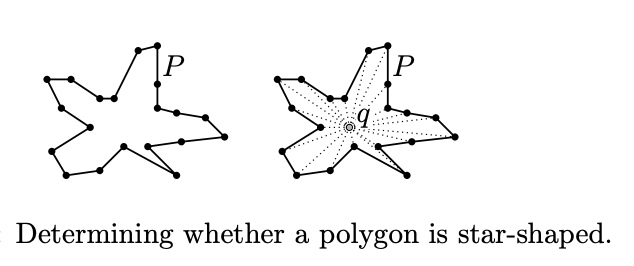
We are given as input the vertices of a polygon P. Determine in near-linear time if P is a star. Specifically, determine if there is a point q inside P such that for every point p on the boundary of P, the line segment pq lies in the interior of P. (Src: David Mount) #exportober
We have a campus in the shape of a perfect disk of radius 1 km. We need to open 7 coffee shops so as to minimize the farthest distance anybody has to travel to get coffee. Where should we open the shops? [Src: Puzzle Toad] #exportober
In a directed graph, a king is defined as a node from which all the other nodes are reachable in at most two steps. A tournament is a directed graph that has exactly one edge between any distinct pair of vertices. Prove that every tournament has a king. #exportober
United States Tendências
- 1. #TT_Telegram_sam11adel N/A
- 2. #hazbinhotelseason2 58.9K posts
- 3. Good Wednesday 20K posts
- 4. LeBron 87.2K posts
- 5. #hazbinhotelspoilers 3,745 posts
- 6. Peggy 20K posts
- 7. #DWTS 54.6K posts
- 8. #InternationalMensDay 25.4K posts
- 9. Baxter 2,321 posts
- 10. Kwara 180K posts
- 11. Dearborn 244K posts
- 12. Reaves 8,980 posts
- 13. Grayson 7,171 posts
- 14. Patrick Stump N/A
- 15. Whitney 16.5K posts
- 16. MC - 13 1,092 posts
- 17. Orioles 7,367 posts
- 18. Sewing 5,136 posts
- 19. Cory Mills 10.2K posts
- 20. Tatum 17.3K posts
Talvez você curta
-
MIT CSAIL
@MIT_CSAIL -
Stanford NLP Group
@stanfordnlp -
Zico Kolter
@zicokolter -
Christopher Manning
@chrmanning -
Chelsea Finn
@chelseabfinn -
Sander Dieleman
@sedielem -
The Abel Prize
@abel_prize -
Deccan Chronicle
@DeccanChronicle -
TensorFlow Community
@TensorFlo -
Isabelle Augenstein
@IAugenstein -
Irene Chen
@irenetrampoline -
Grant Snider
@grantdraws -
Anupam Gupta
@anupamg -
Eren
@kazakerkegi -
Ryan Williams @rrwilliams.bsky.social
@rrwilliams
Something went wrong.
Something went wrong.