English
English Indonesia Türkçe Deutsch Español Português Pусский Français Italiano Nederlands Polski العربية ไทย Tiếng Việt 繁體中文 简体中文 日本語 한국어
math_heiho's profile picture. B3/Essencer

V⊗W

@math_heiho

B3/Essencer

224Posts 69Followers 111Following
Pinned
math_heiho's profile picture.
V⊗W
 @math_heiho
Jun 8, 2024

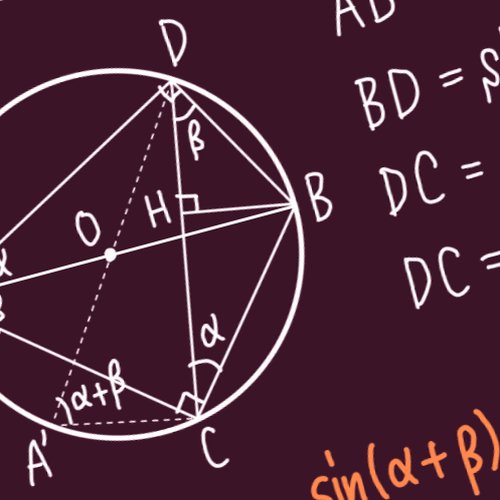
私より数学できる人なんていくらでもいるし、数学は好きだけど私より好きで私より数学を本気で勉強してる人もいくらでもいると思うけど、何か私は数学に対して途轍もない可能性と面白さを感じている。

0
0
20
0
2K
math_heiho's profile picture.
V⊗W
 @math_heiho
Oct 28

確率解析か理論統計(情報幾何)のどちらの研究室にするか悩む🪂

0
0
2
0
50
math_heiho's profile picture.
V⊗W
 @math_heiho
Oct 20

下の方が埋め込まれてる感じかするから単射‼️（適当）

kurobokudo's profile picture. 神戸大学理学部数学科B4(編入)/#spm29th 数学基礎論 /フォロー外しはご自由に/ツイ消しは甘え(自戒を込めて
クロボク
 @kurobokudo
Oct 20

いまだにどっちが全射か単射か迷うんですが、どうやってイメージづけてます？下は分かりませんが、上の方は全射よりも単射に見えるんですよね…

kurobokudo's tweet image. いまだにどっちが全射か単射か迷うんですが、どうやってイメージづけてます？下は分かりませんが、上の方は全射よりも単射に見えるんですよね…
9
6
95
27
24K
0
0
1
0
64
math_heiho's profile picture.
V⊗W
 @math_heiho
Oct 19

これある種の一致の定理だよなー 複素解析の一致の定理で「嘘だろこれ⁉️」ってなった後にこれを見せられたら「まあ嘘ではないかもな」と思える。

kyodai_exam_lab's profile picture. 📚ほぼ毎日、勉強に役立つ情報を発信中！ 🎓京大の過去問をホームページで自由に解説しています。 👨‍🏫大学受験指導も受付中(https://t.co/nHELNLoM62)。 💬質問やリクエストは、DMまたはマシュマロまで(https://t.co/DRTmftEWIj)。 答えられる範囲で答えますので、お気軽にどうぞ😊
京大過去問研究所
 @kyodai_exam_lab
Oct 18

【多項式の一致】 n次以下の多項式f(x)とg(x)が、相異なるn+1個のxについてf(x)=g(x)となるなら、任意のxについてもf(x)=g(x)と言えます。 以下はn=2の場合の証明で、一般のnの場合も同様に証明できます。 [証明] f(x)とg(x)は2次以下の多項式で、x=x₁, x₂, x₃でf(x)=g(x)となるとする。…

0
1
70
38
6K
0
0
2
0
658
math_heiho's profile picture.
V⊗W
 @math_heiho
Oct 1

行く前は想像より新幹線の料金が高くて萎えてたけど、行ってみたらめっちゃ楽しかったし色々な話を聞けた。数物セミナー自体初めてで最初は右も左も分からなかったけど、行ってよかった数物セミナーAdv。もっと早くから行っておけばよかった。

0
0
3
0
127
math_heiho's profile picture.
V⊗W
 @math_heiho
Oct 1

これ本当に嫌い。 小学生の時に以下の図形から平行四辺形を選べって問題で、長方形や正方形も選んだらバツにされた。それ以来初等幾何に対する変な苦手意識が残った。そのままズルズル引きずって、高校の数学教師がベン図で説明してくれてやっと自分は間違っていなかったんだなと確信が持てた。

0315_osami's profile picture. 名前の由来は、自分や他人の中にある弱い声を聞くという意味です。 広島県の古民家で猫２匹と、ボードゲームとマンガが沢山ある塾をやっています。 趣味は海外ビールとボードゲームとマンガとカポエイラ。 色んなところにコメントを付けに行きますが、発言に他意はありません。
よわむし
 @0315_osami
Sep 30

小２だと、正方形が四角形であることが分かる子はまずいないってことになるが？ （犬が動物であることも分からないのか？）

4
6
59
3
38K
0
16
20
2
2K
math_heiho's profile picture.
V⊗W
 @math_heiho
Sep 26

飛行機と新幹線は未だになんか好きでテンション上がるわ。けど乗るときは「わたくしこれに興味ありません(笑)」みたいな顔して乗ってる。

0
0
2
0
35
math_heiho's profile picture.
V⊗W
 @math_heiho
Aug 15

物理の本ではリプシッツ連続を仮定していないのに解の一意性は成り立つし、関数の定義域が連結開集合と明記していないのに導関数が0なら定数関数になる💢

0
0
2
0
76
math_heiho's profile picture.
V⊗W
 @math_heiho
Aug 6

多価関数←関数ではない

ysmemoirs's profile picture. 昼間は黒板の前で数学のような何かを10代の若者と1対40で語り合う人。2012年頃から「#絶対フォント感」を自称しはじめたフォント地層学徒。趣味の数学教育／言語／ラジオ番組／フォント／鉄道／ゲームの話あたりを深夜放送のテイストで。※「このフォント何ですか」をDMでいただいた場合は全体にポストしてお答えします
すど
 @ysmemoirs
Aug 5

群数列　←群とは関係ない 三角関数の合成　←合成関数とは関係ない 逆関数　←逆・裏・対偶とは関係ない あと「数学における術語の用途外使用」何かありますか

15
39
602
81
70K
0
0
4
0
177
math_heiho's profile picture.
V⊗W
 @math_heiho
Jul 24

ローラン展開の主要部求める問題すき

0
0
0
0
66
math_heiho's profile picture.
V⊗W
 @math_heiho
Jul 21

ホモロジー群はかなり理解できたのでヨシ‼️

0
0
1
0
61
math_heiho's profile picture.
V⊗W
 @math_heiho
Jul 21

めっちゃ基本的な線形代数の表現行列についてなんか勘違いしてた… 1年の頃に真面目にやってなかったのが悪いんだけど、自信なくす…

0
0
3
0
102
math_heiho's profile picture.
V⊗W
 @math_heiho
Jul 19

課題の問題どうやっても示せないなーと思ってたら、実数なのに複素数でやってたからだった😿実数でやったらすぐ終わったわ

0
0
0
0
58
V⊗W reposted
math_heiho's profile picture.
V⊗W
 @math_heiho
Feb 9

《群の分類あるある》 位数18、やってること謎。

0
1
1
0
160
math_heiho's profile picture.
V⊗W
 @math_heiho
Jul 15

テスト当日の2時くらいにして環論の面白さに目覚め、なんとかやりきった…❗️今日はゆっくり寝ます🛌

0
0
3
0
114
math_heiho's profile picture.
V⊗W
 @math_heiho
Jul 14

Geminiに聞いたりして軽くまとめた ℤ/nℤってnが素数か合成数かでこんなに性質が変わるんだな😮

math_heiho's tweet image. Geminiに聞いたりして軽くまとめた ℤ/nℤってnが素数か合成数かでこんなに性質が変わるんだな😮
0
5
54
10
3K
math_heiho's profile picture.
V⊗W
 @math_heiho
Jul 13

wikiに載ってるこれ、めっちゃわかりやすくて神✨️

math_heiho's tweet image. wikiに載ってるこれ、めっちゃわかりやすくて神✨️
0
2
7
1
321
math_heiho's profile picture.
V⊗W
 @math_heiho
Jun 9

まだできていない🐑ただ山は越えた(?)

math_heiho's profile picture. B3/Essencer
V⊗W
 @math_heiho
Jun 7

今日明日で単体複体のホモロジー群が理解できそう🐑

0
0
1
0
240
0
0
2
0
178
math_heiho's profile picture.
V⊗W
 @math_heiho
Jun 9

B3 にしてBolzano–Weierstrassの定理の威力に感動してる…

0
0
2
0
127
N_Y_Big_Apple's profile picture. 理系のはず。 サクソフォンと数学を少々。アイコンは@N_Y_Big_Apple作 一応京大数学科の学部を卒業してゐる ジャンプルーキー:https://t.co/9n95tQ5teW pixiv: https://t.co/Tufp73QQEK

N.Y(6/7 ZINEフェス埼玉 4階A 30)

@N_Y_Big_Apple
yukie1728's profile picture. 私は京都大を定年退職して名誉教授になりました。東北大で客員研究員になり、非常勤講師もします。専門は代数群の整数論，概均質ベクトル空間の研究をしています。私はあまり頻繁に twitter を更新はしないと思いますが，ときどき何か書こうと思います。

雪江明彦

@yukie1728
yuzu_pon18's profile picture. 一生モラトリアム

N浪人(N→∞)

@yuzu_pon18
marmot1123's profile picture. カタカナでマーモット/理工展62制作編集/キャンツア/サマチャレ9素核/数物合宿12,13,15,Ad5,6/ぶつどい4/学問/数学/物理/PC/ネット/数学も物理もできない博論書き

marmot1123

@marmot1123
suubutu_PR's profile picture. 数物セミナーは数学・物理に興味のある学部生を主体とした交流を主な目的とした団体です！イベント(談話会、合同合宿)の最新情報を発信していきますヽ(´▽｀)/ follow＆RTお願いします！お問い合わせは↓のホームページよりお願いします

数物セミナー公式アカウント

@suubutu_PR
sN5t1vaIrS34077's profile picture. とある大学院のM2 専門は結び目🪢 Khovanov homologyを頑張ってたりする

ひよっこ。

@sN5t1vaIrS34077
alg_topo's profile picture. 数学科　B4

ゆず

@alg_topo
pi0531018's profile picture. 阪大数学科B2 #spm29th 関数解析 🫶→@megater_0

L’Hôpital

@pi0531018
totomityann's profile picture. M1 / 雑談と数学と健康 / @Akito_ut🍤

とと

@totomityann
Ryuusuu_Iyo's profile picture. 京理B2、数学系志望。有機化学も好き colors！ レゴ同好会所属

留数定理

@Ryuusuu_Iyo
bellestoiles's profile picture. 衒学趣味用(非理学B3)/無言フォロー失礼いたします/何度もフォローしたりしてたらすみません

くものす

@bellestoiles
KogaSense's profile picture. オンラインでの教育アウトリーチします。量子力学、解析力学、その他、マンツーマンで教えます。お持ちの教科書の輪読もOK。大学生、高校生、社会人、誰でも可。完全無料。スカイプまたは他SNS使用。英語もOK。@KogaSense をメンションして直接質問してください。　https://t.co/eN5hpH6yAY…

物理数学なんでも相談室（任意団体）

@KogaSense
gonta_capybara's profile picture. ■微分積分・線型代数・統計学の問題集解いてます。■データ分析も再開しました■物性物理学(修士卒)出身の数学徒■製造業で測定・分析を担当するエンジニア■休日はテニスとお菓子を楽しんでます

ごんた

@gonta_capybara
skinny_navy's profile picture. scienceTokyoB4 代数トポロジーを専攻してます。言語モデルとエージェント開発にも興味があります。節操がないです。お仕事は下記のリンクからお願いします！タマネギ開発中、上野代数幾何

Skinny Navy(スキネビ)@タマネギ開発

@skinny_navy
wasada256's profile picture. 理工

わさだ

@wasada256
n96754660436's profile picture. 慶應お利口学部

ジム

@n96754660436
itamiagari664's profile picture. 慶應b2

ひ塾

@itamiagari664
doctor_cosu's profile picture.

ْ

@doctor_cosu
00harly's profile picture. いのちだいじに

はる

@00harly
gikodaigakuyo1's profile picture. ボブらない

ぎーこ

@gikodaigakuyo1
ayasan1114's profile picture. おもったことをつぶやきます♪

あやさん

@ayasan1114
Ekoro7766's profile picture. IG76th→Keio_st 管理工学科　 意思決定論/詩的な何か 進捗→@ekoro_Shimac764

Ekoro,

@Ekoro7766
nao8086's profile picture. でんじょー/塾生情報局 さいきんの趣味はレトロpc修理、クレカ、旅行など

なお

@nao8086
nay0r0's profile picture. 慶應理工情報工 普段はここにいます → @ma_tw

なよろ

@nay0r0
_vjl2's profile picture. ゆっくりしてます。Abstract Algebra lover

あさしん

@_vjl2
darumayotsu's profile picture. 数学関係、テニス選手、ランナー、保険関係ばかりフォローしている壮年。 PB:full 3h24m(別大23), 100k 11h30m(飛騨高山23)、最長は上州武尊山128k(23、33h) アクチュアリー会準会員、統計検定1級、DSエキスパート、数検1級等。 推しはクロミちゃん、おジャ魔女あいちゃん。

だるまよつくコ:彡

@darumayotsu
math_ldadao's profile picture. 数学用のアカウントを作ってみました。

考え中

@math_ldadao
ATDY6GzGZoYWRWz's profile picture. ミレニアムサイエンススクール所属 | @AnjuYokoi3, @math_yuuka_bot

accept色数accept

@ATDY6GzGZoYWRWz
RcD0VYuQg2grjmL's profile picture. 阪大理学部数学科 B4 🔖🌌

あゆむと！@学べていない、ことばかり

@RcD0VYuQg2grjmL
HKTmine's profile picture. 漢検準一級 応用情報 エルデシュ数5 いっぱい数学イベントに参加したい！ 興味あるイベント：ロマンティック数学ナイト/日本お笑い数学協会/日曜数学会/数学カフェ/プログラマのための数学勉強会/MATH POWER/数学デー/KIOI STEAM LAB/すうがく徒のつどい/数物セミナー/数学ミニプレゼン/むぐむぐ勉強会

ヘカテー

@HKTmine
math_particle's profile picture. 頑張ります💪

猫用

@math_particle
sonukg4india's profile picture. An INDIAN, interested in MATH

SKG

@sonukg4india
to_manifold's profile picture. 大学生数学科4年、幾何学に興味あり、代数幾何ひよっこ入門者、行間が埋まるたびに生を実感する、 #spm29th 層論2 #spmAd7th 可換環論(CM環)

トー

@to_manifold
chris_juravich's profile picture. Although I’m a lawyer, this is a math account. I am a math hobbyist. I love music, sports 🏈 ⚾️ and great books. Cats 🐈 and roses too.🌹 And, mostly, Elina. ❤️

Chris

@chris_juravich
ichi_math's profile picture. （数学）∨（¬（数学））

1

@ichi_math
suyasuyatarina1's profile picture. 東京乗換面倒大学4回生の、眠くてのどカラカラな人です💧｜🎯年齢や所属を問わず新しい人と関わるためのアカウントです｜鍵垢 @uchiwacircle｜アイコン：キラキラ鱈メーカー3 @Zr6Ov様

水分補給🥤とハンドクリーム☁️

@suyasuyatarina1
kyanostat's profile picture. Associate Professor @ The Institute of Statistical Mathematics, Statistics and Machine learning, Statistics for Sciences

Keisuke Yano

@kyanostat
kamadokesh5228's profile picture. 信大23s4。数弱だけど数学は好きです。 鍵→ @kamadokeshi_sub マショマロ→https://t.co/clxmHr8mWz

kamadokeshi

@kamadokesh5228
Kiwamu_Watanabe's profile picture. 中央大学理工。代数幾何。「すごすぎる数の図鑑」発売中：https://t.co/jpAeKfGmKz 数学YouTube：https://t.co/NfanAGVR0k 2018年度建部賢弘賞受賞

渡邉究/数学科准教授/KADOKAWAより「すごすぎる数の図鑑」発売中/YouTube

@Kiwamu_Watanabe
flasca_495's profile picture. 数学をやっています/HMS/mtg/beatmania Ⅱdx/うつ病寛解気味

ふらすか

@flasca_495
tota_toukei's profile picture. みやもととうけい（tota）｜統計学・データサイエンス｜統計検定®︎｜Udemy™登録延べ11万人🙇‍♂️

みやもととうけい（tota）

@tota_toukei
Ryuta953418's profile picture. 現状リツイートオンリー こっちはツイートオンリー@kuripon_desu4

R(最終話)

@Ryuta953418
realrekei's profile picture. 大阪大学大学院 工学研究科 電気電子情報M1 /物性(超伝導)の研究

匿名大学院生

@realrekei
7serei2's profile picture. 阪大理物2回生。

7serei

@7serei2
gami_phys's profile picture. *Hokkaido Univ. phys. B4/nonequilibrium statistical physics/quantum information

gami*

@gami_phys
keio_st's profile picture. 慶應義塾大学理工学部の公式Twitterアカウントです。 Keio University Faculty of Science and Technology【Official】 ご質問やご意見等にはこのアカウントでは対応しておりませんのでご了承ください。

慶應義塾大学理工学部【公式】

@keio_st
toukei_kentei's profile picture. 「統計検定」は、統計に関する知識や活用力を評価する全国統一試験です。

統計検定（公式）

@toukei_kentei
shokabo_editors's profile picture. 自然科学書出版 裳華房 編集部です。読者のみなさまに評価していただける良質な書籍づくりを目指しています。本作りの現場から、本や書店に関する情報を幅広くつぶやきます。裳華房公式のアカウントはこちら（@shokabo）。

裳華房 編集部

@shokabo_editors
tradingMaxiSL's profile picture. Empowering minds, Sharing valuable knowledge and insights to elevate your world. DM for credit / removal

Wolf of X

@tradingMaxiSL
atsueigo's profile picture. TOEIC (LRSW) 満点、英検１級、IELTS8.5、TOEFL114点、VERSANT満点、豪州永住権保持、元米国公認会計士・豪州勅許会計士、オーストラリア国立大学院卒→デロイトオーストラリア(マネージャー)→独立 YouTube 登録者数65万人突破。DM質問不可

ATSU

@atsueigo

United States Trends

Something went wrong.


Something went wrong.