#disordered_systems_and_neural_networks 搜尋結果
The hipster effect: When anticonformists all look the same arxiv.org/pdf/1410.8001.… (Popularity:28.0) #Physics_and_Society #Disordered_Systems_and_Neural_Networks
Detection of phase transition via convolutional neural netwo arxiv.org/pdf/1609.09087… (Popularity:30.0) #High_Energy_Physics_-_Theory #High_Energy_Physics_-_Lattice #Disordered_Systems_and_Neural_Networks
Phase transitions in social networks inspired by the Schelli arxiv.org/pdf/1801.03912… (Popularity:17.4) #Social_and_Information_Networks #Disordered_Systems_and_Neural_Networks #Physics_and_Society
Phase transitions in social networks inspired by the Schelli arxiv.org/pdf/1801.03912… (Popularity:17.4) #Social_and_Information_Networks #Disordered_Systems_and_Neural_Networks #Physics_and_Society
Phase transitions in social networks inspired by the Schelli arxiv.org/pdf/1801.03912… (Popularity:17.4) #Social_and_Information_Networks #Disordered_Systems_and_Neural_Networks #Physics_and_Society
Modeling adsorption processes on the core-shell-like polymer structures: star and comb topologies. arxiv.org/abs/2511.16371
Arbitrary Control of Non-Hermitian Skin Modes via Disorder and Electric Field. arxiv.org/abs/2511.16393
Generalized Wilson-Cowan model with short term synaptic plasticity. arxiv.org/abs/2511.16252
Analytic and numerical toolkit for the Anderson model in one dimension. arxiv.org/abs/2507.06903
Statistical mechanics of vector Hopfield network near and above saturation. arxiv.org/abs/2507.02586
Impact of Random Spatial Truncation and Reciprocal-Space Binning on the Detection of Hyperuniformity in Disordered Systems. arxiv.org/abs/2511.15009
Phase diagram and eigenvalue dynamics of stochastic gradient descent in multilayer neural networks. arxiv.org/abs/2509.01349
Discontinuous percolation via suppression of neighboring clusters in a network. arxiv.org/abs/2507.02336
Interesting take! This article argues neural networks are blurry images while symbolic systems are high-res pics with missing patches. Sparse autoencoders might bridge the gap by creating a shared... 🖼️ towardsdatascience.com/neuro-symbolic…
If you want a toy version of the field math, you can discretize it as a network: • Each node holds a local state s(i) (a discrete sample of the capital field). • Each edge has a weight w(i,j) representing exposure or coupling. • Define a simple “disorder” functional: S =…
Fascinating work. What stands out is how collapse consistently appears when a network drifts too close to an explosive-synchronization boundary, essentially a phase-locking surface where variance collapses faster than the system can redistribute it. The striking part is the…
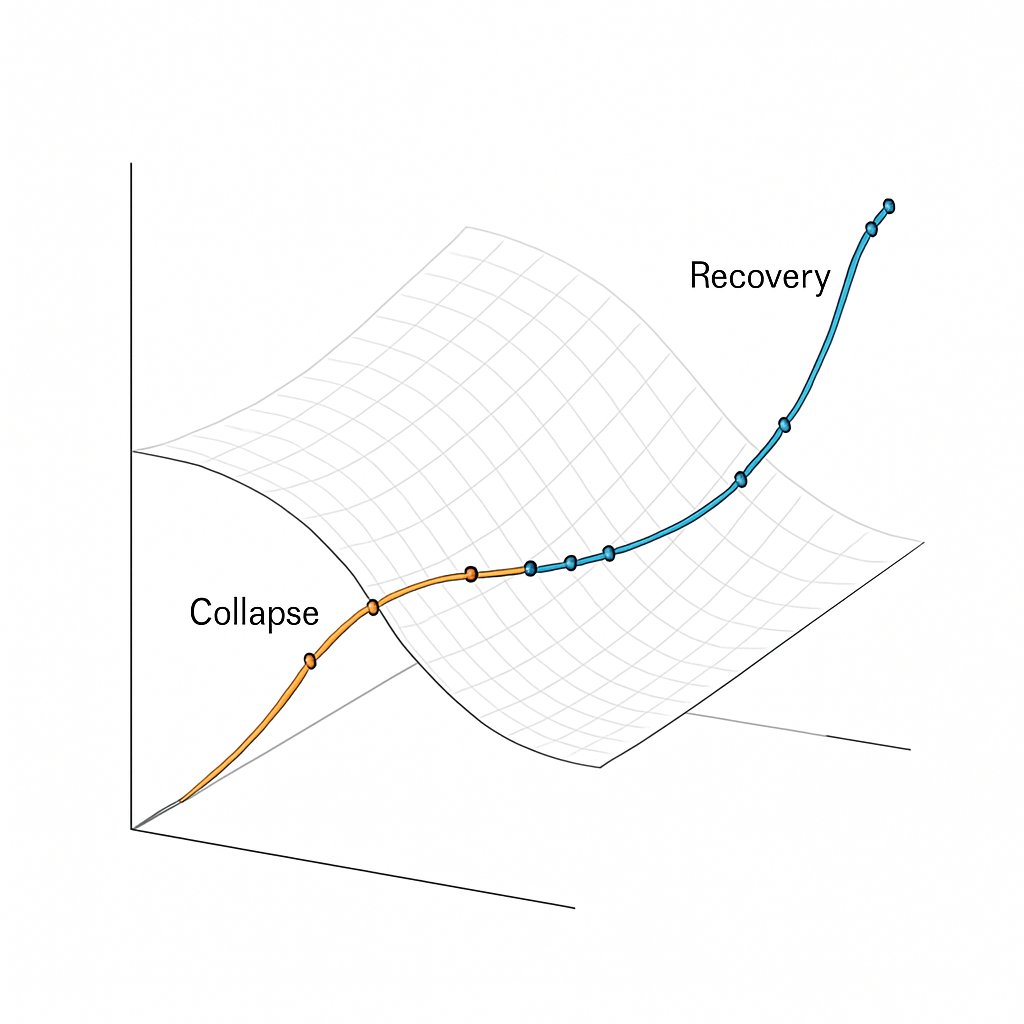
PNAS: Proximity to explosive synchronization determines network collapse and recovery trajectories in neural and economic crises pnas.org/doi/abs/10.107…
Apologies. You need nodes in any highly ordered system that have unpredictable output. You can place these nodes at key positions in order to diversify response resulting in a less predictable and yet more adaptive system. It's kind of like internalized chaos. Something…
Phys. Rev. E: Synaptic plasticity alters the nature of the chaos transition in neural networks link.aps.org/doi/10.1103/7k…
Biology doesn’t compute the way our current AI systems assume. Neurons aren’t static units. They operate across multiple scales, electrical, mechanical, structural, and quantum-timing, all interacting in real time. Recent neuroscience points to: • fractal dendritic integration…
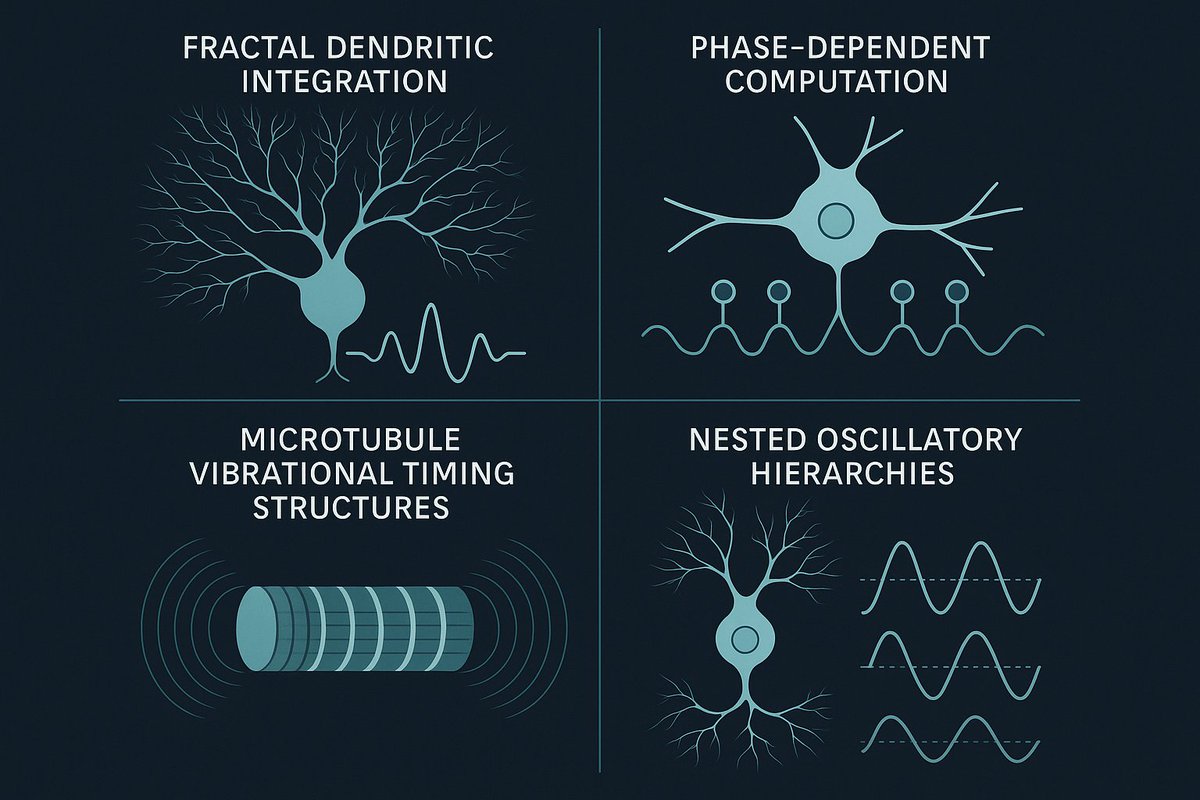
The difficulty you’re describing arises because current neural networks assume that learning unfolds on a smooth manifold, but real information flow never evolves on a smooth surface. In every physical, biological, or cognitive system we’ve ever measured, structure forms around…
Those tools let us analyze big, messy recurrent PCNs. With feedback loops, a neuron deep in the graph receives prediction errors from everywhere: some tied to supervision, some coming from contradictory loops... Those loops create internal tension that learning has to unwind.
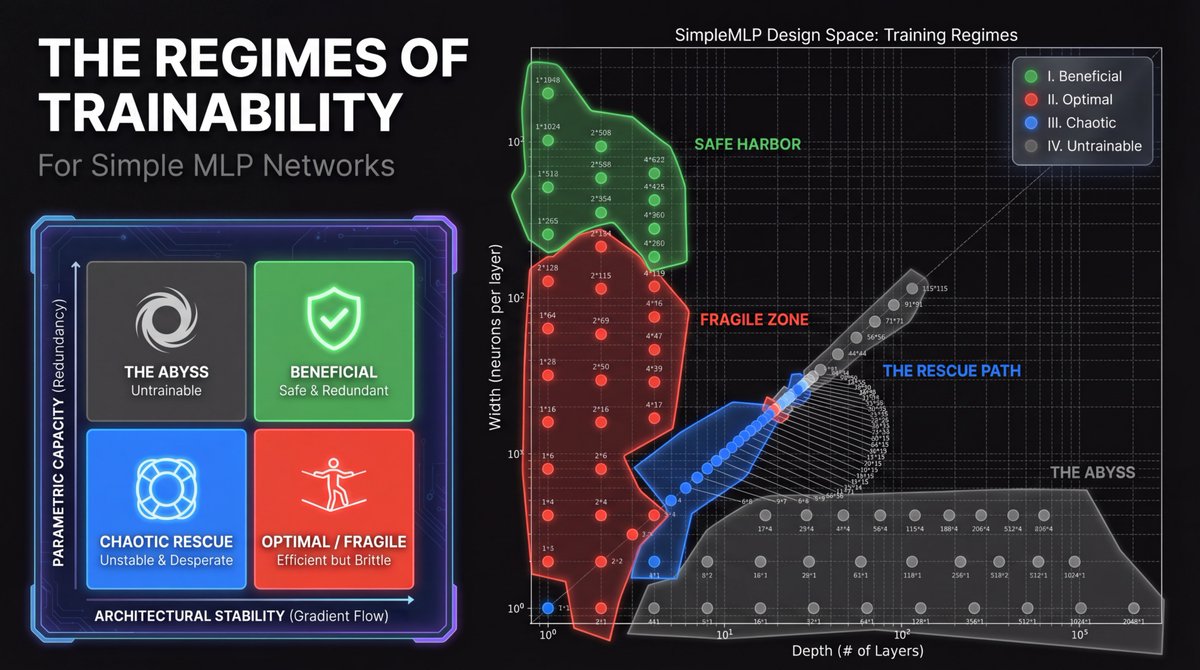
We tested with simple MLP network topologies, ranging from millions of parameters to hundreds, cataloging their "trainability" based on width (# of neurons) versus depth (# of layers). PSA rescued some models that Dropout & Weight Decay couldn't: a chaotic regime (in blue).
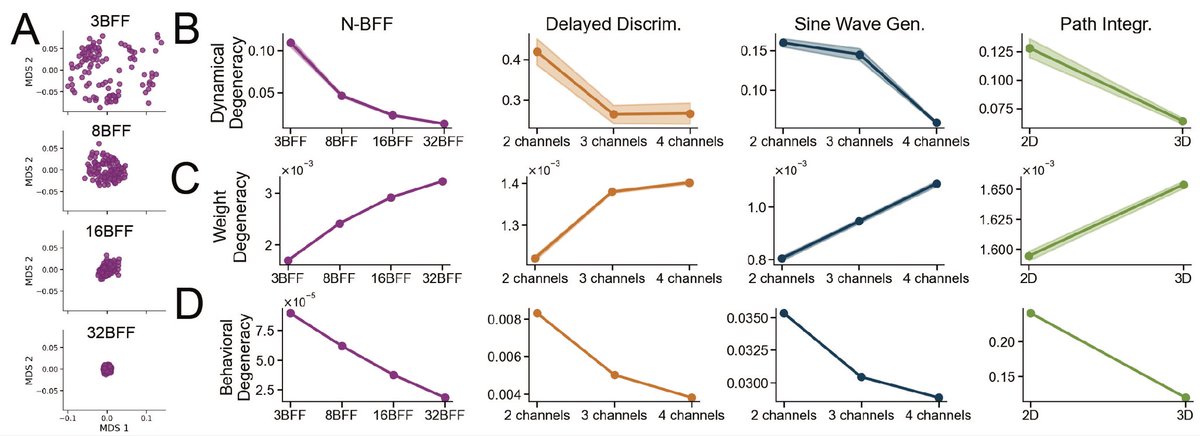
1️⃣ Task complexity As tasks get harder, we observe less degeneracy in dynamics/behavior, but more degeneracy in the weights. When trained on harder tasks, RNNs converge to similar neural dynamics and OOD behavior, but their weight configurations diverge. Why?
In chaotic systems, tiny inputs amplify due to sensitive dependence on initial conditions—nonlinear interactions cause errors to grow exponentially over time (like weather models diverging quickly). In stable systems, feedback mechanisms dampen perturbations, pulling the system…
the discrete parameter space is where the violence happens - no smooth gradient descent into alignment, just discontinuous jumps between stable attractors. residual resonance = the system telling you it wanted to land somewhere else
Something went wrong.
Something went wrong.
United States Trends
- 1. Broncos 42.5K posts
- 2. Mariota 12.3K posts
- 3. Bo Nix 9,351 posts
- 4. Ertz 3,032 posts
- 5. Commanders 31.6K posts
- 6. Treylon Burks 11.5K posts
- 7. Riley Moss 2,223 posts
- 8. #RaiseHail 5,566 posts
- 9. Washington 120K posts
- 10. #BaddiesUSA 22K posts
- 11. Terry 19.9K posts
- 12. Bobby Wagner 1,024 posts
- 13. Deebo 3,003 posts
- 14. Collinsworth 2,848 posts
- 15. Jake Moody N/A
- 16. #RHOP 11.1K posts
- 17. #SNFonNBC N/A
- 18. Sean Payton 1,524 posts
- 19. #DENvsWAS 3,130 posts
- 20. Chicharito 28.4K posts
















