#logarithmicutility نتائج البحث
Me and my team sells premium! We don't know what else to do! #LogarithmicUtility
Utility Functions for Determination of Optimal Variables Understanding how consumers make choices is crucial for analyzing market behavior. Find more here: youtu.be/7M0ksiAY844 #utilityfunctions #logarithmicutility #optimalvariables

Utility Functions for Determination of Optimal Variables Understanding how consumers make choices is crucial for analyzing market behavior. Find more here: youtu.be/7M0ksiAY844 #utilityfunctions #logarithmicutility #optimalvariables

今日の英語 up to 〜の違いを除いて The logarithm is determined up to 2πiℤ. (対数は2πiℤの違いを除いて一意に定まる.)
Logarithm Properties and Rules: A Comprehensive Guide(click to enlarge)...ᝰ.ᐟ

Logarithms are such an integral part of the history of math because of how they made computation a lot faster. For all x, y ∈ ℝ > 0, log(x) + log(y) = log(x·y) based on this, you get faster multiplications [read more: buff.ly/33eUcuk]
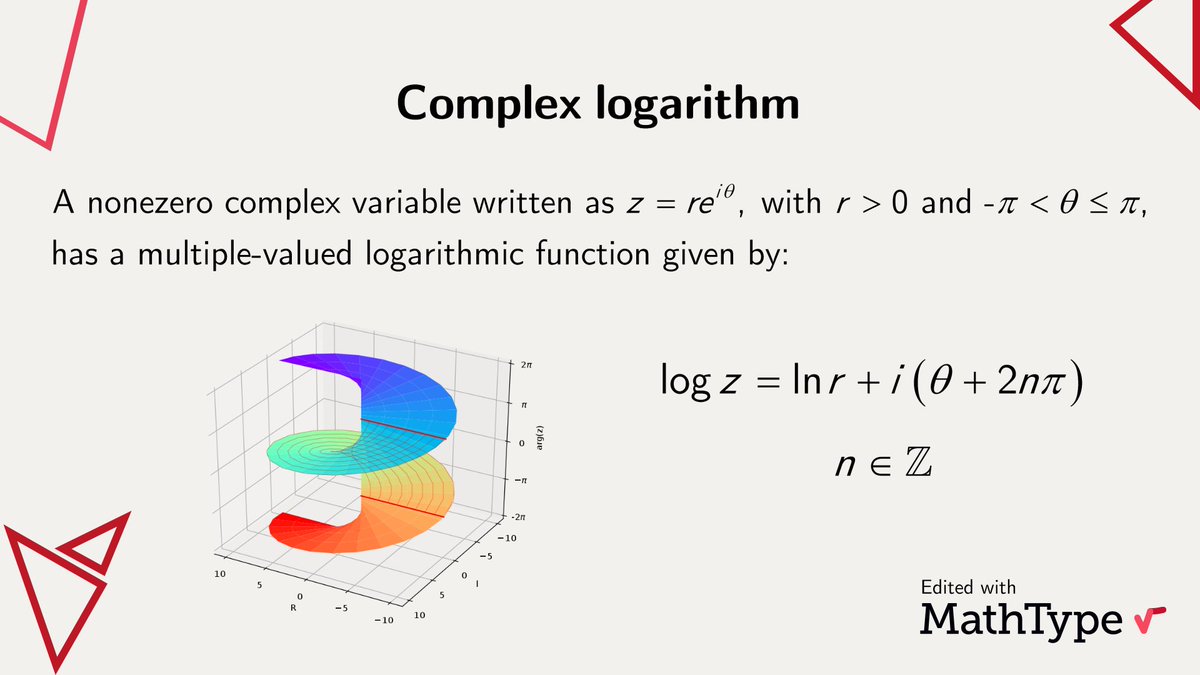
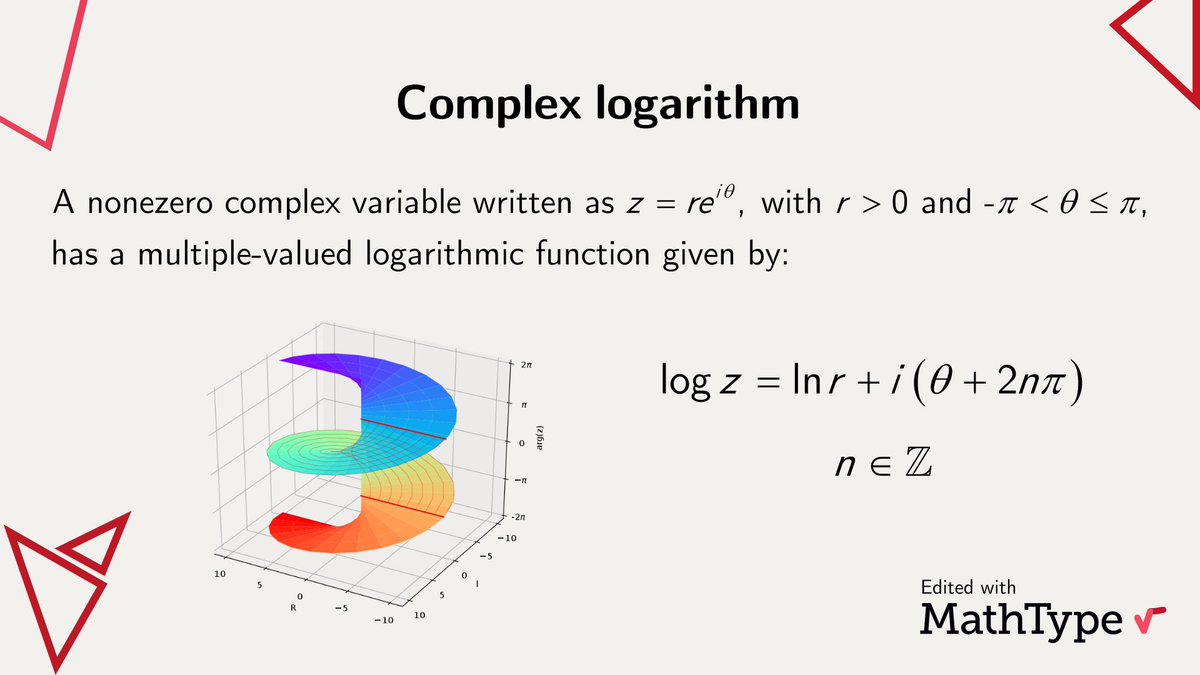
The complex logarithm is the analogue of the logarithm of a positive real number, but for nonzero complex numbers. Similarly, the expression log(0) is left undefined since there is no complex number x such that its exponential gives zero. #MathType
There is one big reason we love the logarithm function in machine learning. Logarithms help us reduce complexity by turning multiplication into addition. You might not know it, but they are behind a lot of things in machine learning. ↓ Here is the entire story. ↓

The complex logarithm is the analogue of the logarithm of a positive real number, but for nonzero complex numbers. Similarly, the expression log(0) is left undefined since there is no complex number x such that its exponential gives zero. #MathType
log(e) is either 1 or 1/ln(10). 1/ln(10) might occasionally come up in a number theory context—particularly from working in base 10.
The main reason that logarithms are such an integral part of the history of math is how they made computation a lot faster. For all positive real numbers x and y, log(x)+log(y)=log(x·y) and based on this, you get faster multiplications [source, read more: buff.ly/33eUcuk]
2 log 3 log (5 log p) = 2 log 1 3 log (5 log p) = 3 log 3 5 log p = 3 p = 5^3 = 125 5 log 2 log (3 log q) = 5 log 1 2 log ( 3 log q) = 2 log 2 3 log q = 2 q = 3^2 = 9 p/q = 125/9
Let i^i = x. log x = i log i e^(iπ/2) = i, so log i = iπ/2 and i log i = -π/2 x = e^(-π/2) ≈ 0.2079
Logarithms are exponents. Nothing more. Nothing less. Hope this helps my Ss better see this fact for themselves. 👀 geogebra.org/m/wqmpavbx @geogebra #MTBoS #ITeachMath #math #mathchat
There is one big reason we love the logarithm function in machine learning. Logarithms help us reduce complexity by turning multiplication into addition. You might not know it, but they are behind a lot of things in machine learning. Here is the entire story. 🧵 👇🏽

This is a logarithm. You'll see it in a lot of machine learning formulas, computer science, and math in general. Here's a really simple explanation of how it works. 🧵 👇🏻

Maybe related: log_2(171!) = 1,026.7873… About time someone had the the guts to declare any binary number with over 1,024 digits to be infinity.
It's known in theory that log(log(n)) approaches infinity, but no one has ever observed it in practice.
Utility Functions for Determination of Optimal Variables Understanding how consumers make choices is crucial for analyzing market behavior. Find more here: youtu.be/7M0ksiAY844 #utilityfunctions #logarithmicutility #optimalvariables

Something went wrong.
Something went wrong.
United States Trends
- 1. #WWENXT 6,637 posts
- 2. Notre Dame 29.4K posts
- 3. Notre Dame 29.4K posts
- 4. Bama 19.7K posts
- 5. Jaylen Brown 2,688 posts
- 6. Paul Dano 4,158 posts
- 7. Van Epps 105K posts
- 8. Ament N/A
- 9. Cam Boozer N/A
- 10. #CFPRankings N/A
- 11. Thomas Haugh N/A
- 12. Behn 61K posts
- 13. #TADCFriend 2,566 posts
- 14. Hugo Gonzalez N/A
- 15. Tarantino 10.9K posts
- 16. Penn State 20.7K posts
- 17. Meechie Johnson N/A
- 18. Stirtz N/A
- 19. Vandy 11.3K posts
- 20. Josh Hart 1,111 posts