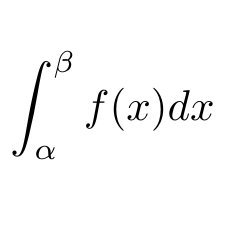내가 좋아할 만한 콘텐츠
座標平面上の2つのベクトルa↑=(p,q),b↑=(r,s)に対して、函数〈a↑,b↑〉を次で定める。 〈a↑,b↑〉=∫[-1→1](px+q)(rx+s)dx (1)〈a↑,b↑〉をp,q,r,sで表せ。 (2) 次の不等式を証明せよ。また、等号の成立条件を述べよ。 〈a↑,b↑〉^2≦〈a↑,a↑〉･〈b↑,b↑〉
長軸と短軸の長さがそれぞれ2a,2bの楕円がある。その周上の点Pにおける楕円の法線と楕円の交点のうち、Pで無い方の点をQとする。線分PQの長さの最小値を求めよ。 (M45/T1 宮城県塩竈市鹽竈神社)
nは自然数とする。関数f(x)の第n次導関数をf^(n)(x)で表し、関数H_n=H_n(x)をH_n=(-1)^n e^(x^2) f^(n)(x)e^(-x^2)と定義する。 (1) n≧3に対してS_n(a)=∫[0→a]xH_ne^(-x^2)dxをH_(n-1)(a),H_(n-2)(a),H_(n-2)(0)により表せ。 (2) n=6の時lim[a→∞]S_6(a)を求めよ。 (H24 中央大)
曲線y=logx上の点Aにおける接線と法線のy軸との交点をB,Cとする。次を求めよ。 (1) △ABCの外心の座標 (2) △ABCの外接円の半径の最小値 (H23 信州大)
OA=OB=1で∠AOB=θの△OABがある。また、OP↑=sOA↑+tOB↑(s^2+t^2≦1)で定義される動点Pがある。 (1) Pの存在領域Dを図示しその面積を求めよ。 (2) 辺ABの中点をMとし、Oを通り直線OMとなす角θで交わる直線をLとする。DをL周りに回転させて得られる立体の体積を求めよ。 (フォロワー提供)
(1) ある投手Oは毎回150gの球を165km/hで投げることができる。球速がOの体格と球の重さに比例するとすれば、第二宇宙速度で投球できる場合、Oと球はどのように変異されるべきか？ (2) (1)のOが地球をちぎって1分間隔で投げる時、地球がバラバラになるのにかかる時間を秒単位で求めよ。 (頭脳王プレ)
空間の8点 O(0,0,0),A(1,0,0),B(1,2,0),C(0,2,0),D(0,0,3),E(1,0,3),F(1,2,3),G(0,2,3) を頂点とする直方体について、O,F,辺AE上の点P,辺CG上の点Qの4点が同一平面上にあるとする。四角形OPFQの面積を最小ならしめるP,Qの座標と四角形OPFQの面積Sを求めよ。 (R3 京都大)
任意の体について、その上の2次元線型変換を考える。表現行列全体の集合をMとし、そのうち正則なものの集合をRとする。 集合Xの濃度を|X|と表すとき、|R|/|M-R|と1はどちらが大きいか。
惑星Xは完全な球形である。ここで、地図をX表面の図を平らな紙に写したもの、その正確性をX表面に沿って測った任意のX上の2点間距離とその2点に対応する地図上の2点間距離の比が常に一定であることと定義したとき、その下でXの正確な地図を作ることはできるか。 (フォロワー提供)
実数a,b,cは関係式(☆) a^2+b^2+c^2-10a-11=0 a^2-bc-4a-5=0 を満たす。 (1) (☆)を満たすb,cが存在するのはaがどのような範囲の値であるときか。 (2) a,b,cが(☆)を満たすとき、ab+bc+caの最小値を求めよ。 (S36大阪大)
kは非負零の実数とする。空間内にAB=5、BC=6、CA=7の△ABCの形をした板がある。この板の頂点A,B,Cに長さが6k、7k、5kの糸の一端をそれぞれ取り付ける。糸の他端をある1点に集めて板を吊るすとき、板が水平面となす角度をkを用いて表せ。
2次正方行列A=[(1,-1),(2,5)]に対して行列BをB=2A^4-12A^3+19A^2-29A+37Eで定義する。ただしEは単位行列E=[(1,0),(0,1)]のことである。 (1) 行列Bを求めよ。 (2) 行列Bの逆行列B^-1をAを用いて表せ。 (数検1級)
次の3曲線 F:y=x^4-x^2+6 (|x|≦1) G:y=12/(|x|+1) (|x|＞1) H:y={cos(2πx)}/2+7/2 (|x|≦2) について (1) 函数の増減を調べ、F,G,Hの概形を同じxy平面に図示せよ。 (2) (1)で図示したものが見られる都道府県名を漢字で答えよ。 (3) F,G,Hで囲まれた領域の面積を求めよ。 (H12 静岡大改)
座標平面において媒介変数t(0≦t≦2π)を用いて x=cos2t y=tsint と表される曲線Cがある。 (1) Cの概形を図示せよ。 (2) Cによって囲まれる図形の面積を求めよ。(H20東京大)
実数yに対してyを超えない最大の整数を[y]と表す。正の実数pに対してJ(p)を以下のように定義する。 J(p)=lim[m→∞]∑[k=1→m] {√p/m^(2p+1)}[(m^2-k^2)^p] 極限値lim[n→∞]J(n)J(n-1/2)を求めよ。
遺伝子疾患DはX染色体上にある遺伝子の変異による劣性形質でありY染色体には存在しない。 Dに罹患している父親を持つDに罹患していない女と、Dに罹患している父親を持つDに罹患していない男の子供がDに罹患している確率を、子供が男と女の場合についてそれぞれ求めよ。
球、円すい、直方体の3種類の立体が複数個存在している。ただし、球の半径、円すいの半径、円すいの高さ、直方体の辺はすべて実数rの整数倍とする。この立体群の体積の合計が10r^3となる組合せは何通り存在するか。ただし円周率は3とし、立体は少なくとも1以上存在するものとする。 (H31東京藝術大)
United States 트렌드
- 1. Warner Bros 80.2K posts
- 2. Good Friday 49.6K posts
- 3. HBO Max 39.5K posts
- 4. #FridayVibes 3,743 posts
- 5. #FanCashDropPromotion N/A
- 6. #FridayMotivation 3,667 posts
- 7. NO U.S. WAR ON VENEZUELA 1,543 posts
- 8. Paramount 25.9K posts
- 9. Red Friday 3,982 posts
- 10. $NFLX 4,195 posts
- 11. Happy FriYay N/A
- 12. Jake Tapper 53.7K posts
- 13. #FridayFeeling 1,603 posts
- 14. The EU 131K posts
- 15. Cloudflare 38K posts
- 16. Pickens 16.7K posts
- 17. $WBD 1,683 posts
- 18. Discovery Global 1,329 posts
- 19. Happy Farmers 3,137 posts
- 20. So Netflix 21.9K posts
Something went wrong.
Something went wrong.