Unterlogiker: ‘In logic, there are morals.’ Überlogiker: ‘Hail Gödelian immoralism!’
Arithmetisation of syntax is usually realised through Gödel-encoding with prime factorisation, but it’s more complicated within PA. Try to think of a way to express ‘the exponent of prime p in factorisation of n is k’ as a predicate with three variables (p,n,k) in PA’s language.
I will extend this kind of algebraic research to trap music and its microgenres no matter what. 😸
My li’l HoTT bih don’t e’en get ‘nuffa ∞-cats, I’m on’ih ahh in ℚ(ζ₅) ry’wih Goldman Sachs, These speds ain’ provin’ no Collatz, I’m havin’ey ass collapse, Mindless how he fail his algebra class, he not James Ax, He ain’ learn no Artin stacks, yeh, he jus’ a speh wi’no racks.
Zoom in close enough and you’ll spot the 0 bands and 0 hoes he’s been hiding. 🙀🙀🙀
I am a 30-year-old rapper from the streets of Atlanta and ts how I proved that p ∣ Fₚ − (5/p) for a rational prime p ≠ 2, 5.
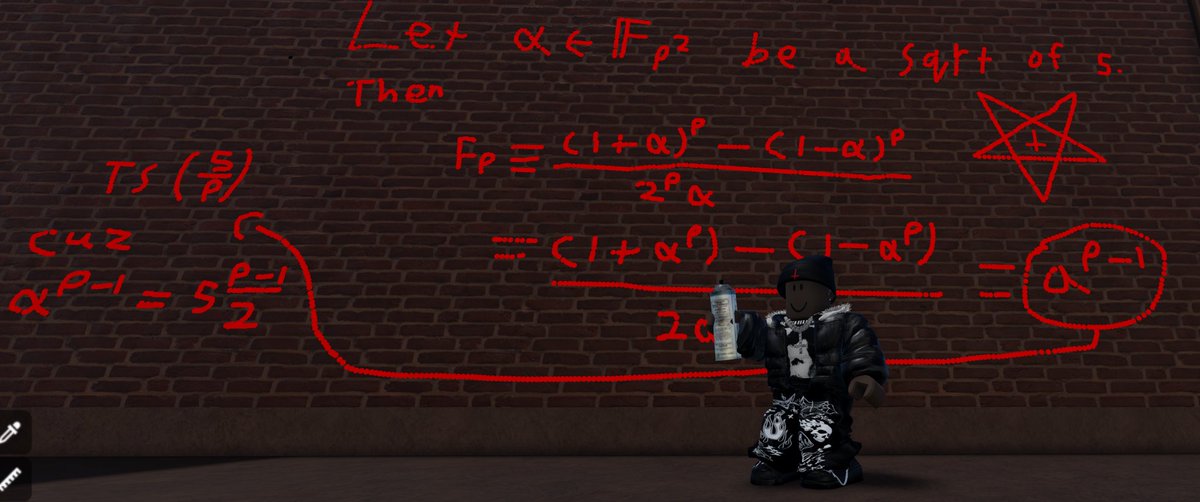
Ain’ no CSB in IZF, it got LEM, He a speh, yeh, his arXiv paper made by a LLM, Étale topoi at 5 AM, homology hoes next, yeh, Now she compute Ext, yeh, Write ha DPhil wit LaTeX, yeh, Put’et bih on ℤ’s Spec, Forced’et ho off’et ℵ₅ trance, Brokies got Springer books financed.
I prove hella shi, I prove like Kurt, She prove π₃(S²) ≅ ℤ, I put that HoTTie in a skirt, Them Martin-Löf hoes tryna flirt, I ain’t intuitionistic, be alert, I take a Cohen real n’ force it hard, ZFC + V = L, got a coanalytic Hamel basis of ℝ, Polytime cut-eliminatin’ Girard.
Balenci’d up when I walk out wi’no field trace, yeh, I’m puttin’ all’ese spedded-up keeds rye’up in’ey place, heh. 😽😽😽
United States 趨勢
- 1. FIFA 435K posts
- 2. Vizio N/A
- 3. Frank Gehry 6,744 posts
- 4. #JingleBellJohn N/A
- 5. Hep B 18.5K posts
- 6. #ROHFinalBattle 2,534 posts
- 7. Hisense 1,248 posts
- 8. $CVNA 1,476 posts
- 9. Paraguay 30.4K posts
- 10. Warner Bros 272K posts
- 11. Portugal 116K posts
- 12. Sherman 5,137 posts
- 13. HOLD THE LINE 6,139 posts
- 14. The EU 234K posts
- 15. Argentina 251K posts
- 16. Matt Campbell 11.3K posts
- 17. Wellington 6,398 posts
- 18. Burden 26.8K posts
- 19. FINALLY DID IT 437K posts
- 20. Iowa State 9,777 posts
Something went wrong.
Something went wrong.