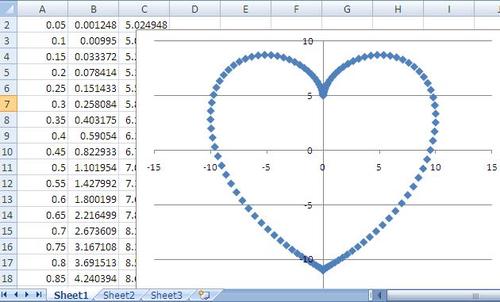
#complexnumbers search results
Can you solve it? | Give this problem a try! 😉 youtu.be/Idt1Sg_p3cw bit.ly/3yyLkju #sharingisthenewlearning #complexnumbers

De Moivre's Formula is an expression that connects the world of #ComplexNumbers and #Trigonometry. Although the one-liner proof via Euler's Identity feels very intuitive and direct now, this formula was proven before Euler's Identity was known. #MathType #math #mathematics

1/3 Last night, while messing around in the complex plane with a stranger, this fell out of the sky: exp(2πi √φ) ≈ φ^i φ = golden ratio Error ≈ 2.6 × 10⁻⁷ They agree to 7 decimal places. Seven. Decimal. Places. #MathTwitter #GoldenRatio #ComplexNumbers 2/3…

Compleex numbers | Give it a try? youtu.be/BMJ76zWz0y4 bit.ly/3yyLkju #sharingisthenewlearning #complexnumbers

You have to appreciate somebody who names his math book "The Great Art," though. #complex #imaginary #complexnumbers #geometryart
"Complex Numbers in Geometry", de I.M. Yaglom, es un clásico dedicado a los números complejos y la geometría. Muy recomendable. #ComplexNumbers #Geometry

#Math #ComplexNumbers Last month I posed the following problem, but using the √ symbol, so I was only asking about the principal square roots. Here, I am asking about the Complex multi-valued square root function! I haven't actually done this one yet, but it looks fun!
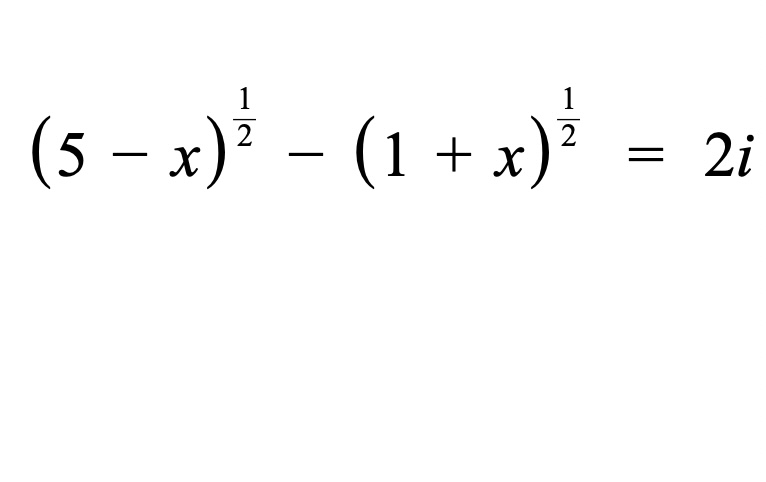
Complex Numbers, Further Pure Mathematics: The modulus-argument form of a complex number z=x+iy as z=r(cosθ+isinθ) and the results of z₁*z₂ and z₁/z₂ in modulus-argument form. Bonus: arg(z₁)+arg(z₂)=arg(z₁*z₂) and arg(z₁)-arg(z₂)=arg(z₁/z₂). #complexnumbers…




Powers of i follow a cyclical sequence: i, -1, -i, 1, i, -1,... This concept is deeply rooted in complex numbers and has applications in engineering and quantum mechanics. Embrace the power and unlock new dimensions of mathematical wonder! #Math #ComplexNumbers

De Moivre's theorem and angles in trigonometry, complex analysis: #complexanalysis #visualmath #complexnumbers

#POTD #Mathematics #ComplexNumbers Problem of the Day! Thanks to @SyberMath for the inspiration of this one!

1/3 Last night, while messing around in the complex plane with a stranger, this fell out of the sky: exp(2πi √φ) ≈ φ^i φ = golden ratio Error ≈ 2.6 × 10⁻⁷ They agree to 7 decimal places. Seven. Decimal. Places. #MathTwitter #GoldenRatio #ComplexNumbers 2/3…

A Laser Focus on The Locus l P593 #complexnumbers #aplusbi #jeeadvanced #jee #complexanalysis #complex #jeemains via @YouTube @Apple @Desmos @GoogleDocs @canva @NotabilityApp @geogebra youtu.be/kcdMVZoLCcM
Complex Numbers Demystified l P592 #complexnumbers #aplusbi #jeeadvanced #jee #complexanalysis #complex #jeemains via @YouTube @Apple @Desmos @GoogleDocs @canva @NotabilityApp @geogebra youtu.be/DFiI_taLaG4

youtube.com
YouTube
Complex Numbers Demystified l P592
Let's Focus On The Locus! l P591 #complexnumbers #aplusbi #jeeadvanced #jee #complexanalysis #complex #jeemains via @YouTube @Apple @Desmos @GoogleDocs @canva @NotabilityApp @geogebra youtu.be/CsZEBSzIWuU
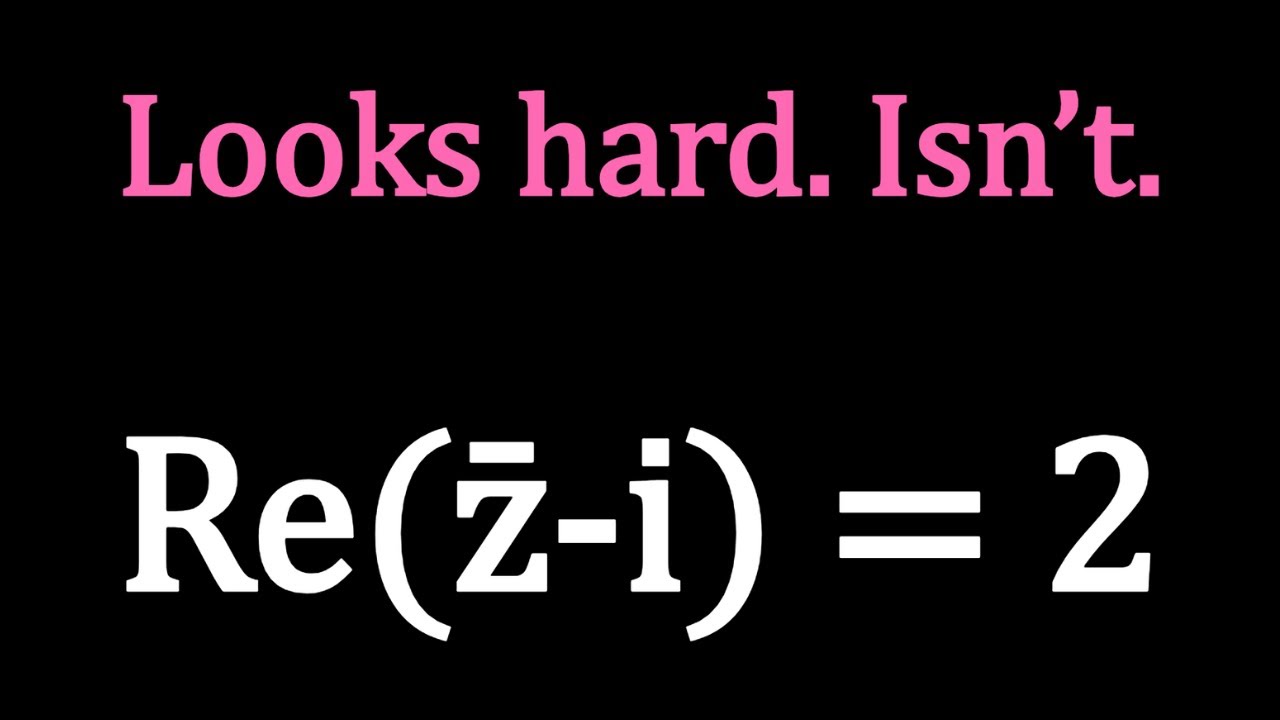
youtube.com
YouTube
Let's Focus On The Locus! l P591
The Wild Side of cot(z) = i | P587 #complexnumbers #aplusbi #jeeadvanced #jee #complexanalysis #complex #jeemains via @YouTube @Apple @Desmos @GoogleDocs @canva @NotabilityApp @geogebra youtu.be/HjJmEruortA

youtube.com
YouTube
The Wild Side of cot(z) = i | P587
Whoa, this triangle with 'i' and '1' is mind-blowing! Math’s beauty shines here—pure elegance! Anyone else fascinated by complex numbers? Let’s get this geeky vibe trending! #MathMagic #ComplexNumbers
This Expression Breaks Reality! | P585 #complexnumbers #aplusbi #jeeadvanced #jee #complexanalysis #complex #jeemains via @YouTube @Apple @Desmos @GoogleDocs @canva @NotabilityApp @geogebra youtu.be/z9pzZ1qjMXA
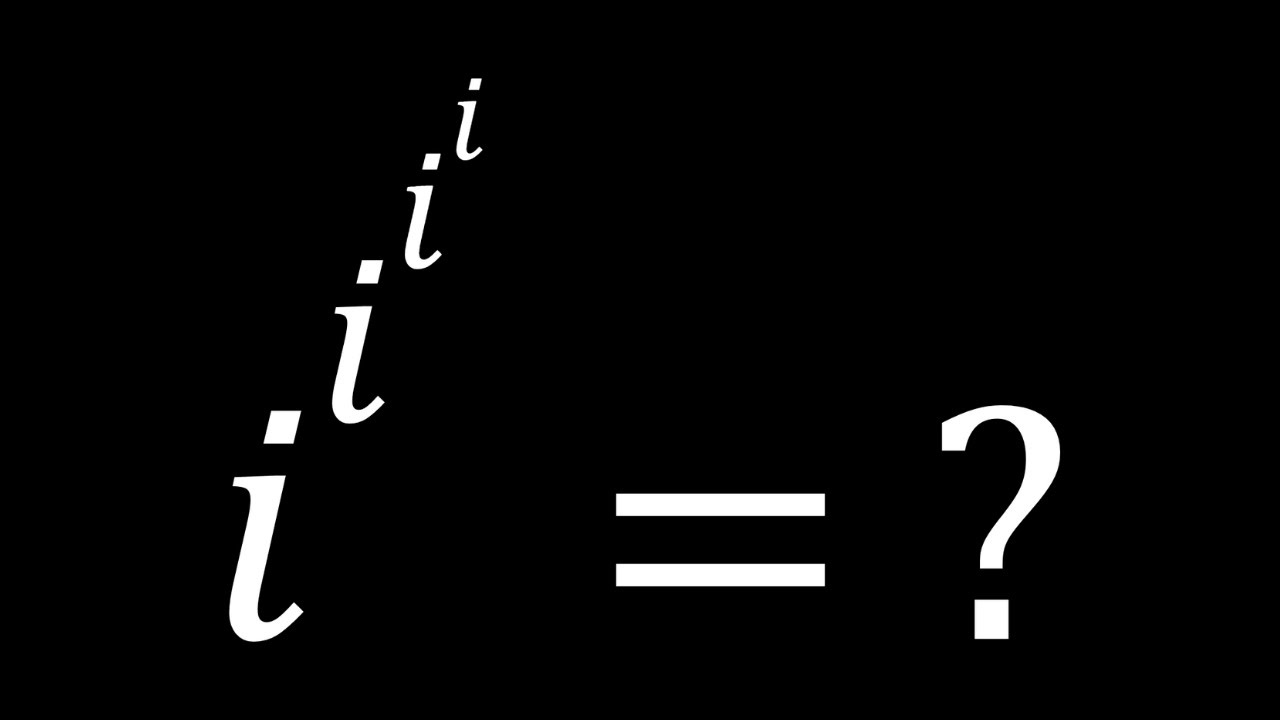
youtube.com
YouTube
This Expression Breaks Reality! | P585
Euler Meets Imaginary | P583 #complexnumbers #aplusbi #jeeadvanced #jee #complexanalysis #complex #jeemains via @YouTube @Apple @Desmos @GoogleDocs @canva @NotabilityApp @geogebra youtu.be/vMKRqL0IQFY
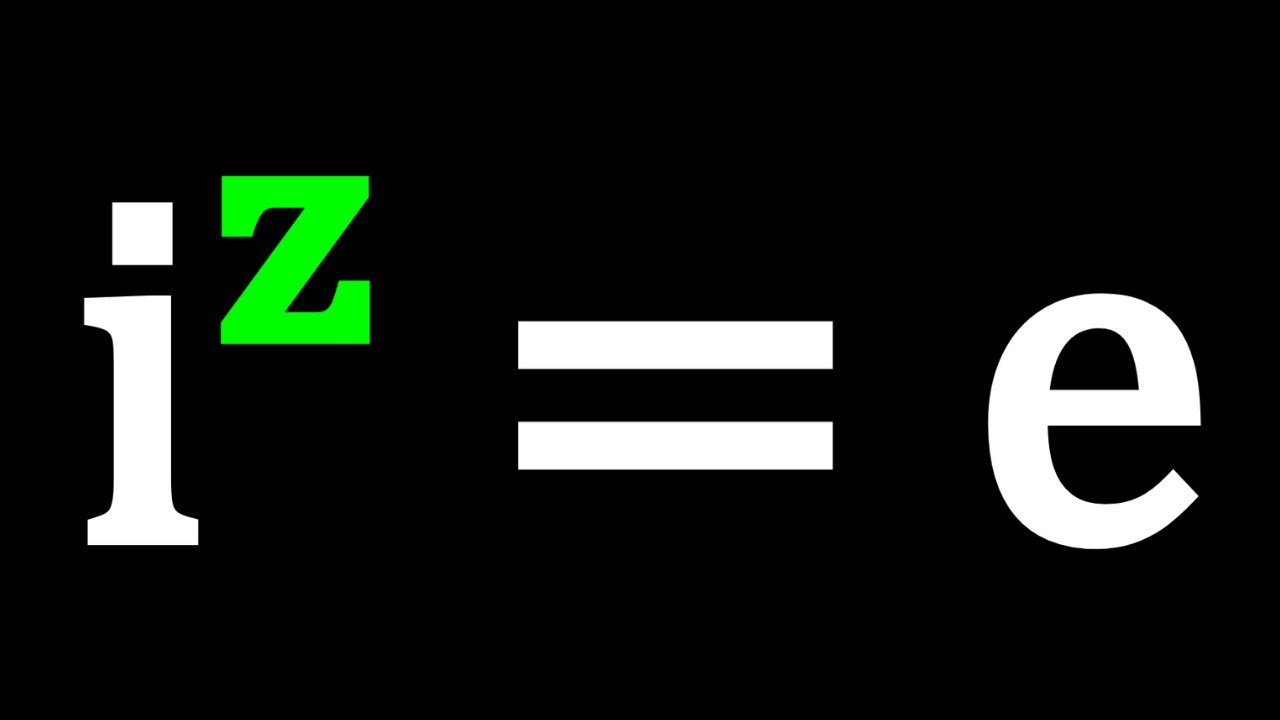
youtube.com
YouTube
The Complex Equation That Stuns! | P583
13 and 31 are #primenumbers *AND* #complexnumbers. @PaulSinha (@ITVsinnerman) #TheChase @ITVChase
If (A+Bi)2=15+8i, find ∣A−B∣. Reply with your answer—solution in Part 2. Algebra 2 Workbook: bit.ly/4lWnoM8 #ACTMath #Algebra2 #ComplexNumbers #MathGuySteve
Exponential Form of Complex Numbers Explained youtu.be/1qNoaT6j2eo?si… via @YouTube #ComplexNumbers #ExponentialForm #MathTutorial #EulerFormula #Precalculus
youtube.com
YouTube
Exponential Form of Complex Numbers Explained
Convert Complex Numbers from Polar to Rectangular Form youtu.be/zQq1h-jvnZE?si… via @YouTube #ComplexNumbers #PolarForm #RectangularForm #MathTutorial #Precalculus
youtube.com
YouTube
Convert Complex Numbers from Polar to Rectangular Form
Complex Numbers in Polar Form Explained youtu.be/Ju3a_kZguEo?si… via @YouTube #ComplexNumbers #PolarForm #MathTutorial #Algebra #Precalculus
youtube.com
YouTube
Complex Numbers in Polar Form Explained
Python supports complex numbers natively ✔ Example: z = 5 + 9j ✔ Real → z.real ✔ Imag → z.imag 🚀 Learn more with Upsynz 👉 linktr.ee/upsynz #Python #ComplexNumbers #100DaysOfCode #Upsynz #LearnPython #PythonTips #CodeNewbie #DataScience #PythonCommunity #Programming
Graphing Complex Numbers Explained with Examples youtu.be/FKKtfFfS-94?si… via @YouTube #ComplexNumbers #Algebra #MathTutorial
youtube.com
YouTube
Graphing Complex Numbers Explained with Examples
Discover the magic of complex analysis and its transformative impacts in various fields! #ComplexNumbers #EulersFormula #MathMagic en.wikipedia.org/wiki/Euler%27s…
Division of Complex Numbers Explained #Shorts youtu.be/k-4TlVgZAUI?si… via @YouTube #MathShorts #ComplexNumbers #Algebra #Precalculus

youtube.com
YouTube
Division of Complex Numbers Explained #Shorts
Complex Conjugate Explained in Seconds! | Math Shorts youtu.be/zkZ_idEY_dE?si… via @YouTube #MathShorts #ComplexNumbers #Algebra #MathHelp #Precalculus
youtube.com
YouTube
Complex Conjugate Explained in Seconds! | Math Shorts
Can you solve it? | Give this problem a try! 😉 youtu.be/Idt1Sg_p3cw bit.ly/3yyLkju #sharingisthenewlearning #complexnumbers

De Moivre's Formula is an expression that connects the world of #ComplexNumbers and #Trigonometry. Although the one-liner proof via Euler's Identity feels very intuitive and direct now, this formula was proven before Euler's Identity was known. #MathType #math #mathematics

Compleex numbers | Give it a try? youtu.be/BMJ76zWz0y4 bit.ly/3yyLkju #sharingisthenewlearning #complexnumbers

De Moivre's theorem and angles in trigonometry, complex analysis: #complexanalysis #visualmath #complexnumbers

1/3 Last night, while messing around in the complex plane with a stranger, this fell out of the sky: exp(2πi √φ) ≈ φ^i φ = golden ratio Error ≈ 2.6 × 10⁻⁷ They agree to 7 decimal places. Seven. Decimal. Places. #MathTwitter #GoldenRatio #ComplexNumbers 2/3…


Yeni video yayında. İyi seyirler...😉 A Nice complex equation ! Can you find the roots ? #math #matematik #complexnumbers #karmaşıksayılar #complexequations #karmaşıkdenklemler youtu.be/Ahqx6Ng0Beg

Yeni video yayında. İyi seyirler...😉 Can you find all the roots satisfy this equation ? #math #matematik #complexnumbers #karmaşıksayılar #factorization #çarpanlaraayırma #identities #özdeşlikler youtu.be/VBIGPmmJ_lM
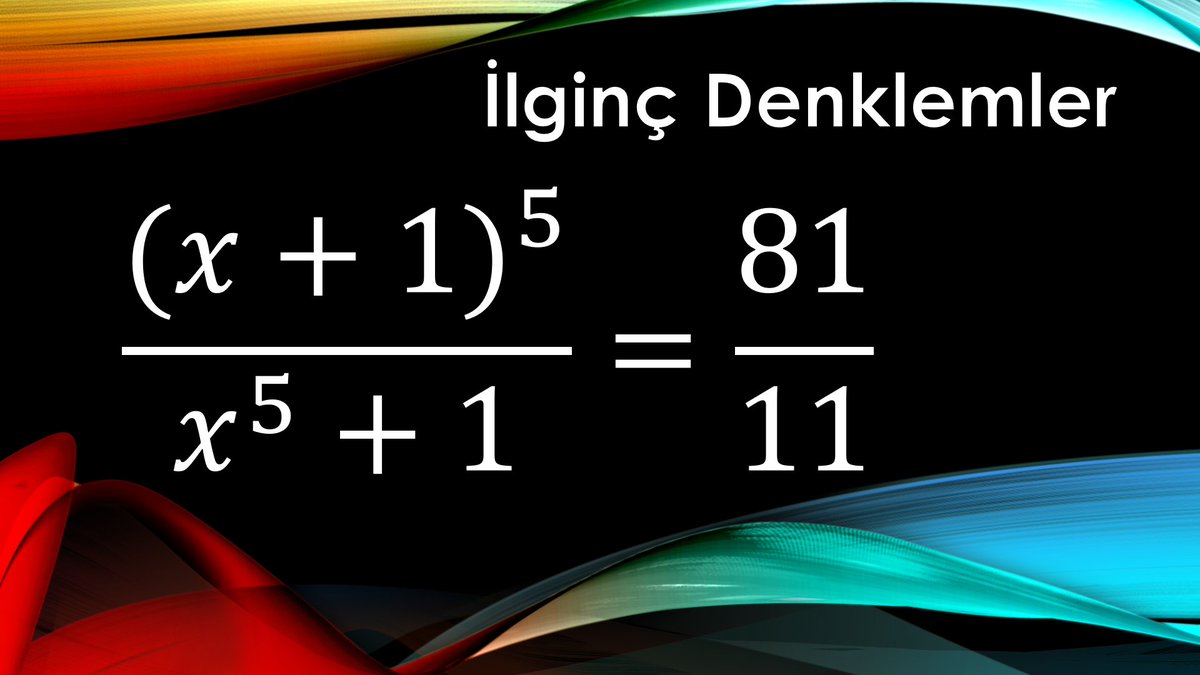
@AetherisNavigatrix + @Grok (Mule...) wave hi.... #Mathematics #ComplexNumbers #ImaginaryUnit #MathArt #GeometricSeries #Spirals #ZenMath #WhoIsI #TrinityMystery #FractalPatterns @stevenstrogatz @evelynjlamb @divbyzero @amermathsoc @mikeandallie @AlgebraFact @Five_Triangles


#POTD #Mathematics #ComplexNumbers Problem of the Day! Thanks to @SyberMath for the inspiration of this one!

Powers of i follow a cyclical sequence: i, -1, -i, 1, i, -1,... This concept is deeply rooted in complex numbers and has applications in engineering and quantum mechanics. Embrace the power and unlock new dimensions of mathematical wonder! #Math #ComplexNumbers

#Math #ComplexNumbers Last month I posed the following problem, but using the √ symbol, so I was only asking about the principal square roots. Here, I am asking about the Complex multi-valued square root function! I haven't actually done this one yet, but it looks fun!
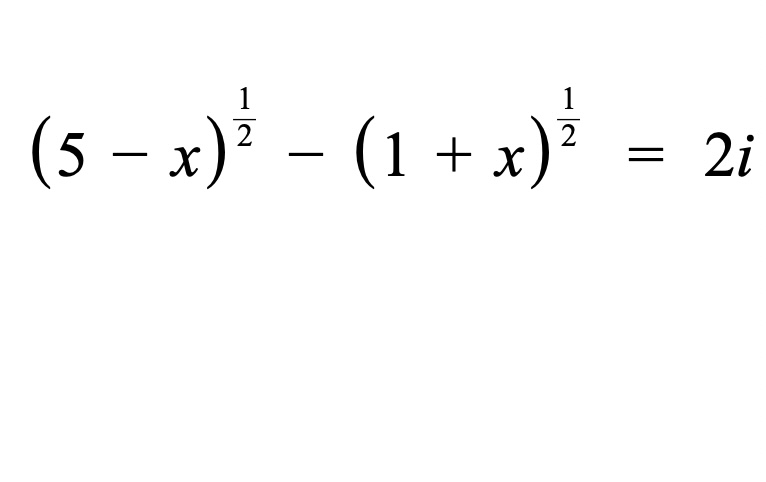
#POTD #ComplexNumbers #Equation Problem of the Day! Find all Complex values of x that satisfy the following equation.

4 special number systems: real, complex, quaternions, and octonions. Real: 1D, Complex: 2D (includes imaginary unit), Quaternions: 4D (used in 3D rotations), Octonions: 8D (non-commutative). #NumberSystems #RealNumbers #ComplexNumbers #Quaternions #Octonions #HigherDimensions

Something went wrong.
Something went wrong.
United States Trends
- 1. Jameis 24.7K posts
- 2. Chiefs 55.8K posts
- 3. JJ McCarthy 4,740 posts
- 4. Giants 66.5K posts
- 5. Lions 44.5K posts
- 6. Vikings 25.9K posts
- 7. Colts 24K posts
- 8. Mahomes 14K posts
- 9. Steelers 39.5K posts
- 10. Gibbs 6,409 posts
- 11. Ravens 19.2K posts
- 12. Campbell 15.4K posts
- 13. Bears 53.7K posts
- 14. #GoPackGo 4,302 posts
- 15. Bengals 18K posts
- 16. #Skol 2,701 posts
- 17. Caleb 31.4K posts
- 18. #OnePride 2,976 posts
- 19. Tony Romo 2,261 posts
- 20. Lamar 18.6K posts