#differentialgeometry risultati di ricerca
Here are some important books about #DifferentialGeometry that will help you learn more and be more interested. Learn with me about the mathematical fabric that affects our world, from the beauty of curves to the mysteries of the universe. 1. Challenge yourself with…

曲線と曲面の微分幾何学. フルテキストがダウンロード可能. #Pogorelov #DifferentialGeometry
Another title that caught my eyes while browsing archive[dot]org for math textbooks translated from Russian was: "Differential Geometry" by "A.V. Pogorelov" A pretty short book (167 pages), but contents seem interesting. Available at: archive.org/details/pogore…
![Riazi_Cafe_en's tweet image. Another title that caught my eyes while browsing archive[dot]org for math textbooks translated from Russian was:
"Differential Geometry" by "A.V. Pogorelov"
A pretty short book (167 pages), but contents seem interesting.
Available at: archive.org/details/pogore…](https://pbs.twimg.com/media/GVuT4aka8AMaypy.jpg)
How about differential geometry once in a while?(たまには微分幾何学でもいかが?) #mathematics #DifferentialGeometry
***Breaking News*** Earth is flat! at least locally - and adding up many small flat areas ends up in a flat surface - at least to good approximation 😉 #differentialGeometry
On August 30, 1819, Joseph Serret was born. He was a French mathematician known for the Frenet–Serret formulas. #DifferentialGeometry #Geometry


🚀 Exciting News! ISDIGA 2025 – International Symposium on Differential Geometry and Applications is happening on July 3-4, 2025! Join top researchers & scholars to explore the latest in Differential Geometry. Stay tuned for updates! 🔗 #ISDIGA2025 #DifferentialGeometry

(Open Access) Differential Geometry: From Elastic Curves to Willmore Surfaces - freecomputerbooks.com/Differential-G… Look for "Read and Download Links" section to download. Follow/Connect me if you like this post. #Geometry #DifferentialGeometry #Topology #math #mathematics

(Open Access) Functional Differential Geometry - freecomputerbooks.com/Functional-Dif… Look for "Read and Download Links" section to download. Follow/Connect me if you like this post. #Geometry #DifferentialGeometry #topology #math #mathematics

Read #FeaturePaper "A Differential-Geometric Approach to Quantum Ignorance Consistent with Entropic Properties of Statistical Mechanics" from Shannon Ray et al. mdpi.com/1099-4300/25/5… #differentialgeometry #entanglemententropy #quantuminformation #statisticalphysics #ignorance

One of the best and easiset book to start learning Curves and Surfaces, first step to Differential Geometry. A complete review with TOC here: youtube.com/watch?v=LorGhy… #differentialgeometry #Math #booklovers #Geometry #noneuclideangeometry

Sometimes, I do miss the good old days in school. 🥲 You can focus on whatever you like. #Relativity #Maths #DifferentialGeometry

📢Pleased to announce our latest work "Riemannian Geometry and Molecular Similarity II: Kähler Quantization" with Stuart Hall, Thomas Murphy (@csuf) and @ColeGroupNCL Now out: arxiv.org/abs/2301.04424 @ChemistryNCL @NCLMathsStats #DifferentialGeometry #chemoinformatics #LBVS
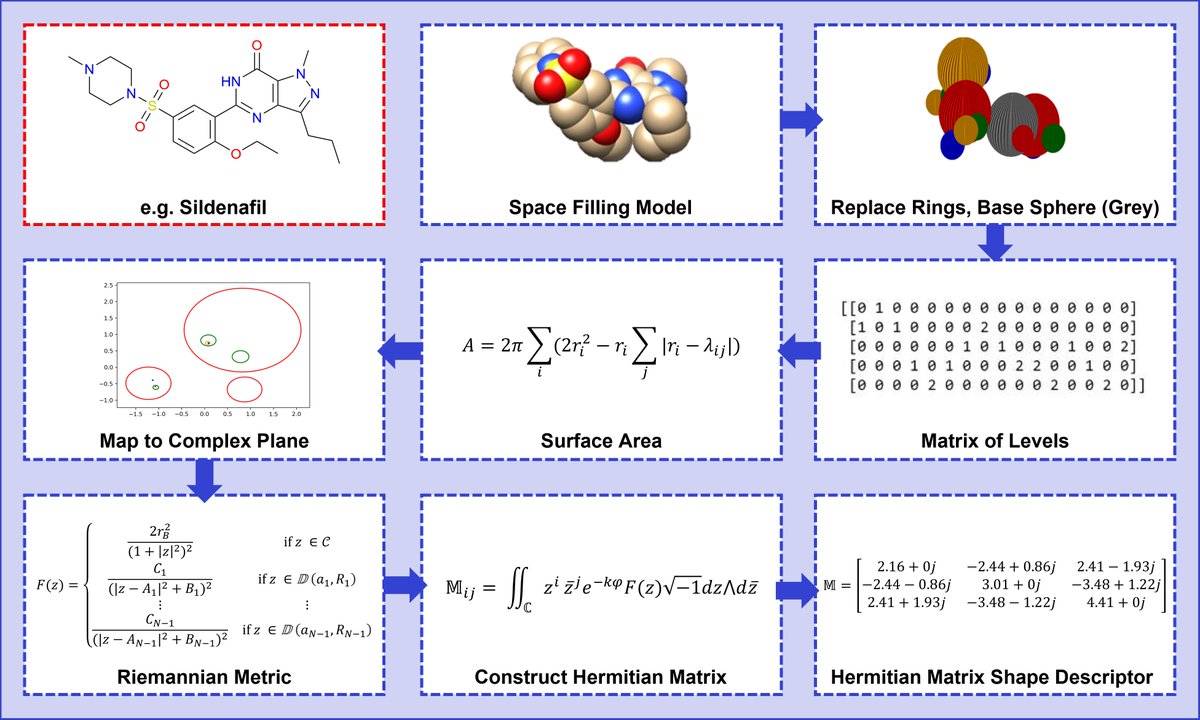
Based on classic #differentialgeometry needed to understand deterministic manifolds Prof. Søren Hauberg showed how to turn the mathematical concepts into simple algorithms that allow for principled #dataanalysis over learned manifolds. #ScaDSAISummerSchool24

Differential Geometry of Curves and Surfaces by Do Carmo 4000TL #differentialgeometry #canonicalform #tangentplane #firstfundementalform #GaussMap #vectorfields #minimalsurface #akademikzam #conformalmap #geodesics #JacobiFields #abstractsurface instagram.com/p/CMHeOreFItq/…
instagram.com
Fatih Gürses (@sadesahhaf) • Instagram photos and videos
Fatih Gürses (@sadesahhaf) • Instagram photos and videos
Embark on a journey to master differential geometry! 🌐 Join Beng and friends as they explore curved surfaces, Ricci curvature, and black holes. Read a free chapter now and discover the beauty of geometry: shorturl.at/2tqFG #DifferentialGeometry #Mathematics
[Book] Lugo's 2021 "Differential Geometry in Physics" is an excellent concise guide, spanning from vector basics to bundle concepts, now freely accessible thanks to the University of North Carolina. libres.uncg.edu/ir/uncw/f/lugo… #DifferentialGeometry #Physics #Math #Education
![AyyoubAkbari's tweet image. [Book]
Lugo's 2021 "Differential Geometry in Physics" is an excellent concise guide, spanning from vector basics to bundle concepts, now freely accessible thanks to the University of North Carolina.
libres.uncg.edu/ir/uncw/f/lugo…
#DifferentialGeometry #Physics #Math #Education](https://pbs.twimg.com/media/GhrgrUIXMAAGpFM.jpg)
Riemann Tensor is one of the ways to find out the curvature of the space. But it's component form is very hard to remember. Is there a trick to remember it?: rousan.netlify.app/pages/physics/… #differentialgeometry #generalrelativity #cosmology #astrophysics #relativity #physics #math
An application of topological invariance of de Rham Cohomology: Let M be a smooth manifold. In each point of M there is a neighborhood such that every closed form is exact. #DifferentialGeometry #Manifolds
楽しそうな雰囲気だけ感じられるdiscrete differential geometryの研究 arxiv.org/pdf/2006.14461… やっぱ時代はDDGでしょう 勉強したことないけど #DifferentialGeometry


Frenet–Serret formulas describe the derivatives of the tangent, normal, and binormal unit vectors of a three-dimensional curve, in terms of each other and the curvature and torsion of the curve. They're key in #DifferentialGeometry. #MathType

Today in 1777, Carl Friedrich Gauss, the prince of mathematics, was born. One of the few mathematical giants that needs no introduction: you will stumble upon #Gauss' name in #Algebra, #DifferentialGeometry, #NumberTheory, and basically most fields in #Mathematics. #MathType
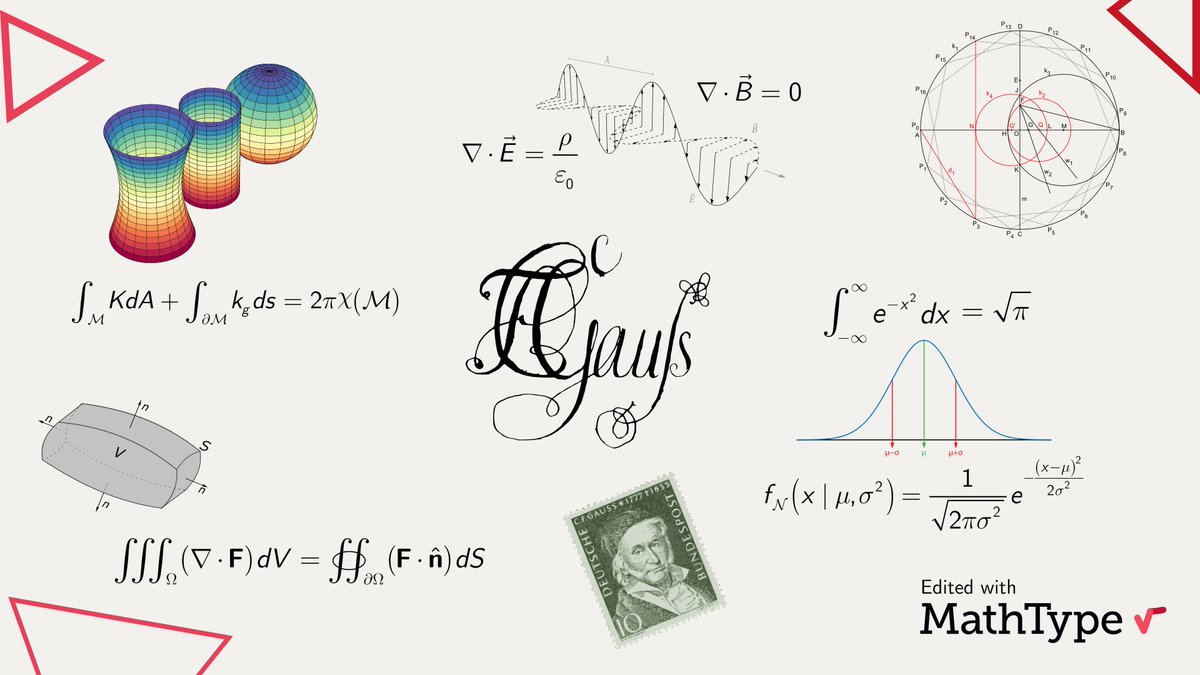
Astonishing feats mark Riemann's career: he gave #NumberTheory the Zeta function and the Riemann Hypothesis, laid the foundations of general relativity with #DifferentialGeometry and gave #Calculus the first rigorous formulation of the integral, the Riemann Integral. #MathType

The Gauss-Bonnet Theorem describes curvature on a surface. It can be used to prove that the angles of any triangle add up to exactly pi rad, but only on a plane. On a sphere they add up to more than pi, on a hyperboloid they add up to less than pi #DifferentialGeometry #MathType

Joseph Antoine Ferdinand Plateau was born today in 1801. He studied the #Physics of soap bubbles. Because soap bubbles form minimal surfaces, the mathematical problem of finding the minimal surface given a boundary in #DifferentialGeometry is called Plateau's Problem. #MathType

The mathematical problem of finding the minimal surface given a boundary in #DifferentialGeometry is called Plateau's Problem, in honor of Joseph Antoine Ferdinand Plateau who studied the #Physics of soap bubbles, that form minimal surfaces. #MathType

Hadamard's Lemma is a close relative to the multidimensional Taylor series expansion. It tells us that smooth functions behave more like polynomials than one might expect, serving as a bridge between #DifferentialGeometry and #AlgebraicGeometry #MathType

Here are some important books about #DifferentialGeometry that will help you learn more and be more interested. Learn with me about the mathematical fabric that affects our world, from the beauty of curves to the mysteries of the universe. 1. Challenge yourself with…

Kitabın yayınlanmasının üzerinden 4 yıl geçti. Bu kitapta ortaya konan fikirler ve kavramlar gelişti ve bağımsız araştırma alanları haline geldi. #geometry #differentialgeometry #manifoldtheory

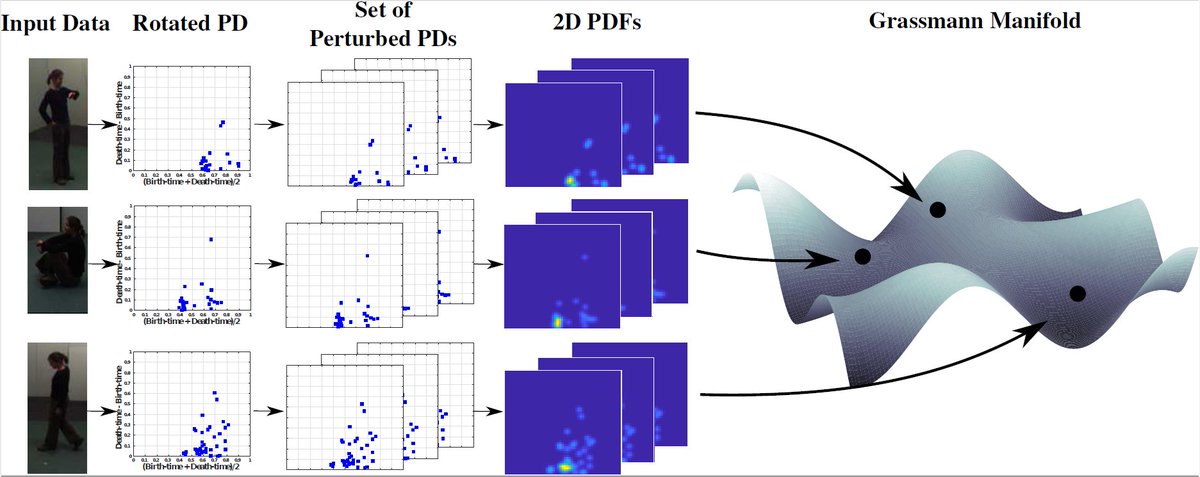
Our paper "Perturbation Robust Representations of Topological Persistence Diagrams" got accepted to #ECCV2018 😀 Paper: arxiv.org/abs/1807.10400 #ComputationalTopology #DifferentialGeometry #ComputerVision #MachineLearning #GeometricMediaLab #ECCV18
Stephen Smale born July 15 #differentialgeometry #math #mathdate #teaching #teachingmath #saturdaymorning
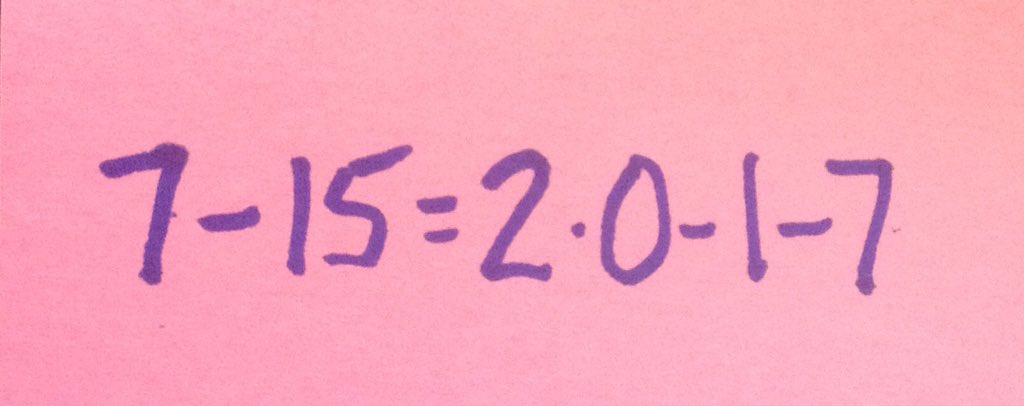
The Gauss-Bonnet theorem talks about curvature on a surface. It also proves that the sum of angles of a triangle is exactly pi, but only on a plane. On a sphere they sum more than pi, on a pseudosphere they sum less than pi #DifferentialGeometry #MathType
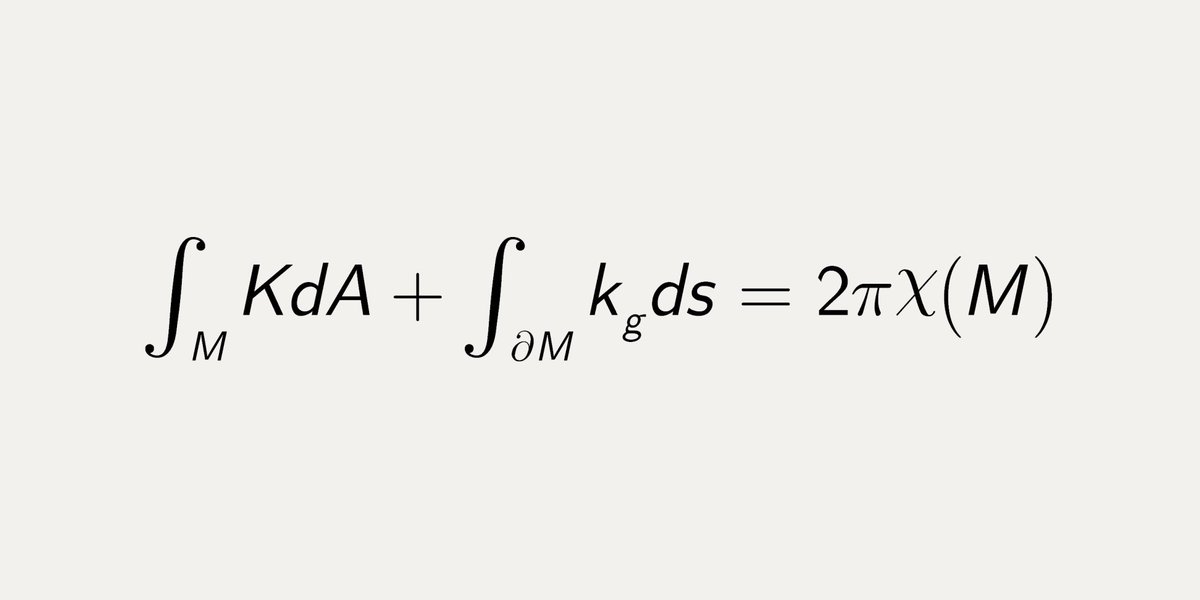
Gravity waves over La Jolla form a one-form pierced by a contrail vector dual. #CloudMath #DifferentialGeometry #Weather

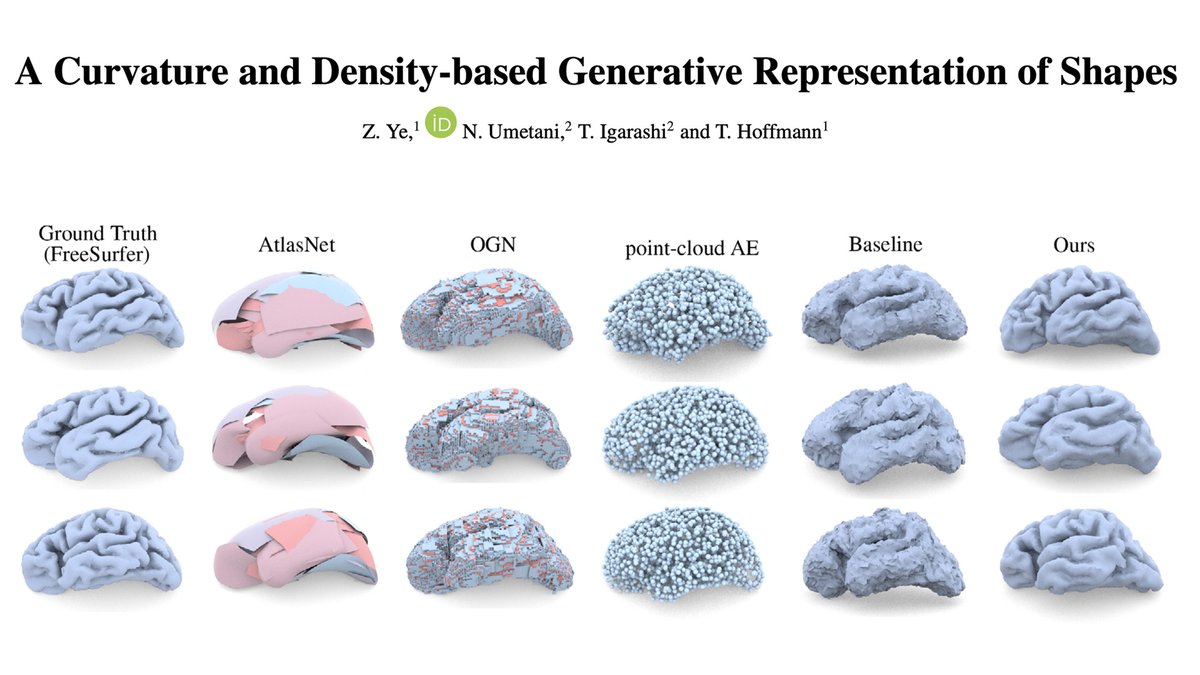
An important idea in #DifferentialGeometry is that curvature provides a shape description that doesn't depend on coordinates. Yet et al use this fact to build a generative model for 3D shapes that captures detailed and highly nonconvex folds and wrinkles: onlinelibrary.wiley.com/doi/full/10.11…
"A portion of the Enneper surface, rotating” by @gregeganSF Source and information: bit.ly/2ensIXf For more: bit.ly/2WxEVz0 #maths #differentialgeometry #algebraicgeometry #EnneperSurface
How about differential geometry once in a while?(たまには微分幾何学でもいかが?) #mathematics #DifferentialGeometry

#SpecialIssue mdpi.com/journal/applsc… DD: 15 November 2021 Guest Editors: Prof. Dr. Krzysztof Kozlowski (1951–2021) and Dr. Dariusz Pazderski #controlofmechanicalsystems #differentialgeometry #linearization #Lyapunovstabilitytheory #trajectoryplanning #multiagentsystems

Gauss-Bonnet is often used as the first example of a "local-global" theorem in #DifferentialGeometry, but there's a much easier one: If you know the total curvature along the boundary of a planar domain, you can deduce the number of holes (n).

Something went wrong.
Something went wrong.
United States Trends
- 1. Good Thursday 25.9K posts
- 2. #thursdayvibes 1,575 posts
- 3. Happy Friday Eve N/A
- 4. #thursdaymotivation 2,064 posts
- 5. #DMDCHARITY2025 1.62M posts
- 6. Merry Christmas 67.9K posts
- 7. Toyota 26.4K posts
- 8. Halle Berry 3,736 posts
- 9. Steve Cropper 8,024 posts
- 10. Omar 181K posts
- 11. Earl Campbell 2,230 posts
- 12. #ALLOCATION 727K posts
- 13. The BIGGЕST 1.03M posts
- 14. #JUPITER 244K posts
- 15. Metroid Prime 4 16K posts
- 16. Market Focus 4,711 posts
- 17. Milo 13K posts
- 18. Mike Lindell 24.6K posts
- 19. seokjin 169K posts
- 20. TPUSA 63K posts

































