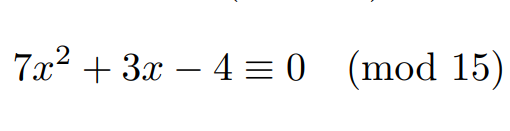#modulararithmetic ผลการค้นหา
Finding the remainder | Give it a try? youtube.com/watch?v=9Y6Wt2… #sharingisthenewlearning #modulararithmetic

Modular Arithmetic "mod" is known as the operator of Modular Arithmetic Given (a)mod(b)=c where a,b,c are integers(±z). Where a is the dividend, b is the divisor, and c is the remainder. #sharingisthenewlearning #mod #modulararithmetic
🔢 LeetCode Daily: Smallest Missing Integer ✅ Modular arithmetic magic! Track remainder frequencies, consume greedily from 0 upward. ⚡ O(n) with mod tracking 🎯 Remainder classes = equivalence 💡 Handle negatives: ((n%v)+v)%v #LeetCode #CPlusPlus #ModularArithmetic

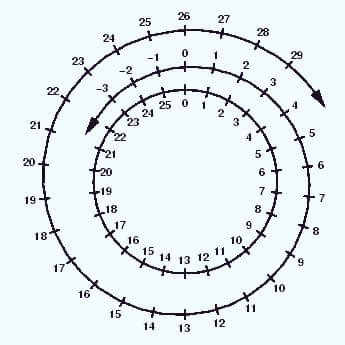
#POTD #Math #ModularArithmetic #Tougher Problem of the Day! Here's a weird one today. Clearly we would never say that 7 = i. However, did you know that 7 is congruent to i, mod 10? That is: 7 ≡₁₀ i. Nice!

#POTD #Math #ModularArithmetic Problem of the Weekend! Here's the last in the series this week. You'll need to put on your thinking caps for at least one part, if not two. There are also (at least) two good ways to attack this one. Have fun!
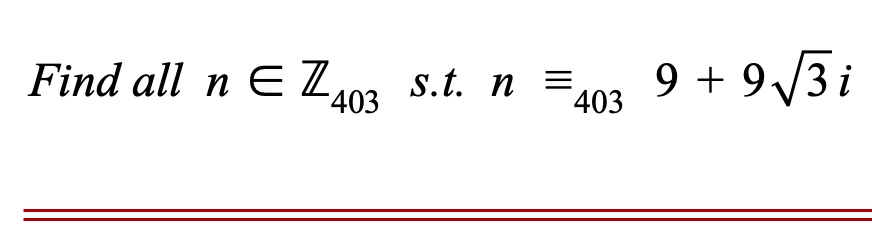
#POTD #Math #ModularArithmetic Problem of the Day! We've been building up to tomorrow's Problem of the Weekend, and today's should be a piece of cake if you were able to make it through yesterday's finding of n's congruent to 𝒊. (I've been looking for the best i: 𝒊? ⅈ? 𝖎?)
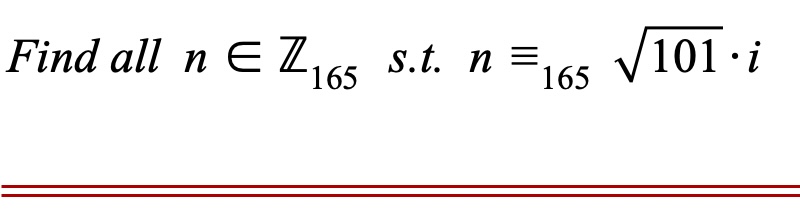
#POTD #Math #ModularArithmetic Problem of the Day! Here's the followup modular arithmetic problem to yesterday's. If you're not already familiar with these, it's time to get your learn on! Extra Hint: there are more than two answers!
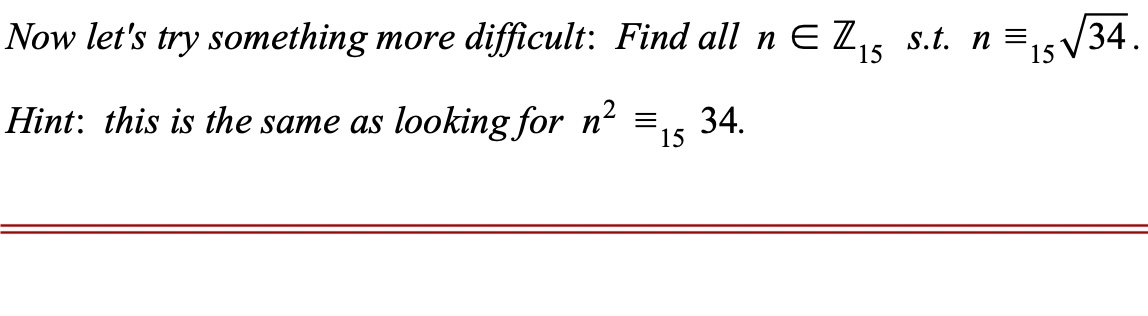
Problem of the Day #69: a ≡ 68 (mod 1967) a ≡ 69 (mod 1968) a ≡ ? (mod 14) Find the remainder of a divided by 14. The solution link is in the bio. #ModularArithmetic #NumberTheory #RemainderProblem #ProblemSolving #ExactScience

Let (G, *) be a finite group. Prove that every element in G must have finite order. *With extra workings for comprehension of the proof. #furtherpuremaths #grouptheory #modulararithmetic


Solved LeetCode's “Count the Number of Arrays with K Matching Adjacent Elements”! 🎯 Applied combinatorics: 🧮 C(n-1, k) × m × (m-1)^(n-k-1) ⚙️ Used fast mod inverse & exponentiation ✅ Great practice for math-based problems! #LeetCode #CodingChallenge #ModularArithmetic
Modular Arithmetic: Studying the nature of the cyclical group ({0, 1, 2, 3, 4}, addition modulo 5). Properties of a Group: Closure ✅ Identity ✅ Inverses ✅ Associativity ✅ #modulararithmetic #furtherpuremaths

#POTD #Math #ModularArithmetic #Simple Problem of the Day! I'll post a solution to the weekend's integral tomorrow. This week will be a brief tutorial on solving some modular arithmetic problems. We're starting off easy, for those who don't know much yet.

Problem of the Day #88: Source: UKMT - Intermediate Mathematical Challenge - 2024 - 16 The solution link is in the bio. #FactorialSum #ModularArithmetic #ProblemSolving #ExactScience #NumberTheory

🔢 LeetCode Daily: Smallest Missing Integer ✅ Modular arithmetic magic! Track remainder frequencies, consume greedily from 0 upward. ⚡ O(n) with mod tracking 🎯 Remainder classes = equivalence 💡 Handle negatives: ((n%v)+v)%v #LeetCode #CPlusPlus #ModularArithmetic

Finding the remainder | Give it a try? youtube.com/watch?v=9Y6Wt2… #sharingisthenewlearning #modulararithmetic

Find the remainder when 2¹⁰⁰⁰ is divided by 13. *Full workings. #furtherpuremaths #modulararithmetic #fermatslittletheorem #alevelmaths
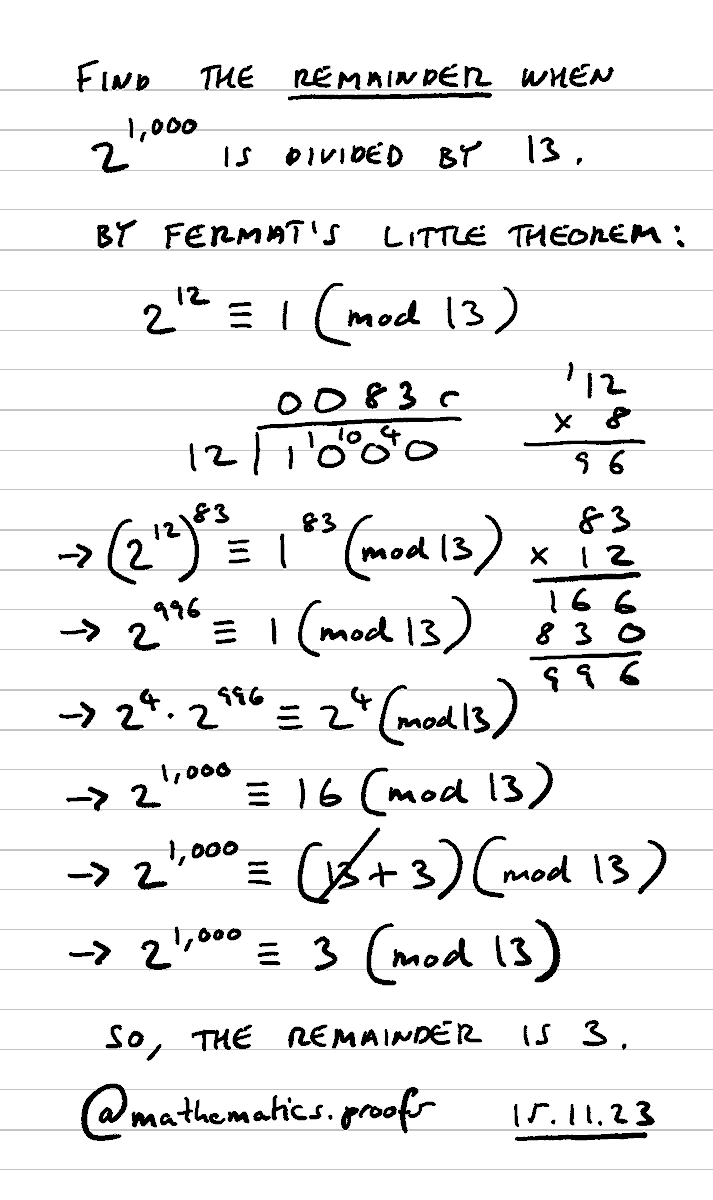
Modular Arithmetic "mod" is known as the operator of Modular Arithmetic Given (a)mod(b)=c where a,b,c are integers(±z). Where a is the dividend, b is the divisor, and c is the remainder. #sharingisthenewlearning #mod #modulararithmetic

Prove that 5²² + 17²² ≡ 6 (mod 11) #furtherpuremaths #modularcongruence #modulararithmetic #fermatslittletheorem
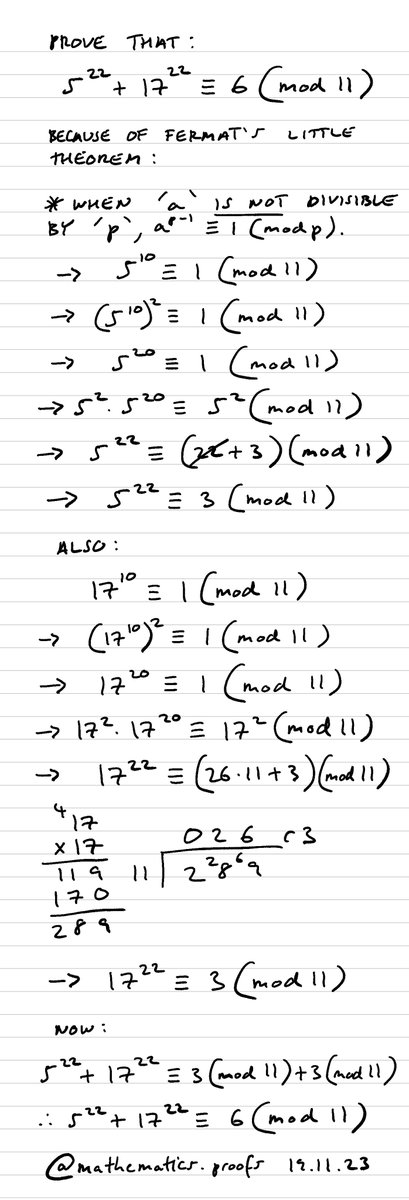
Find the least residue of 3²⁰² modulo 11. #furtherpuremaths #modulararithmetic #fermatslittletheorem #clockarithmetic

(2 Ways) Solve the congruence equation: 75x≡12(mod237) #modularcongruence #modulararithmetic #alevelmaths #furtherpuremaths
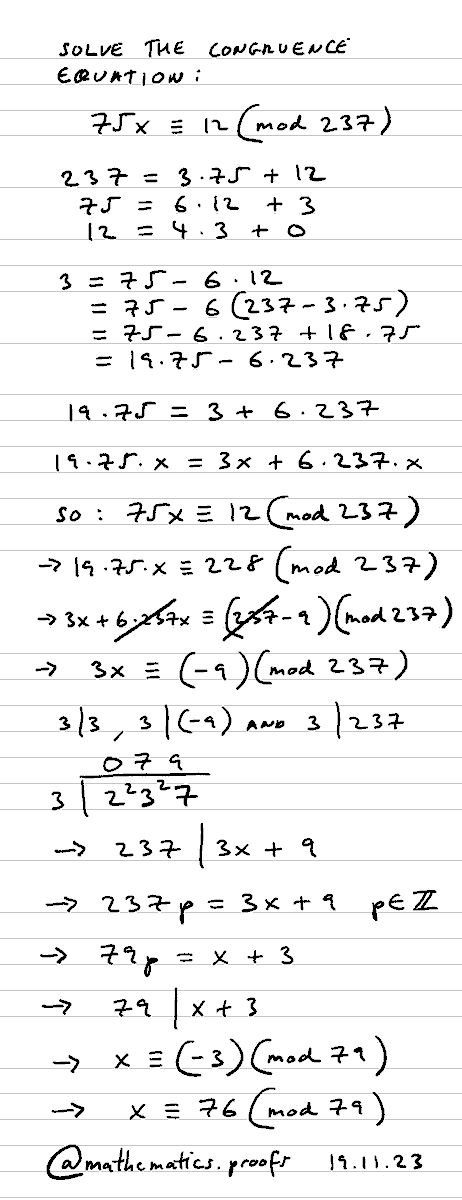

Modular Arithmetic: Studying the nature of the cyclical group ({0, 1, 2, 3, 4}, addition modulo 5). Properties of a Group: Closure ✅ Identity ✅ Inverses ✅ Associativity ✅ #modulararithmetic #furtherpuremaths

Resolving the division anomaly. *Work with integers included. #furtherpuremaths #modularcongruence #modulararithmetic #alevelmaths


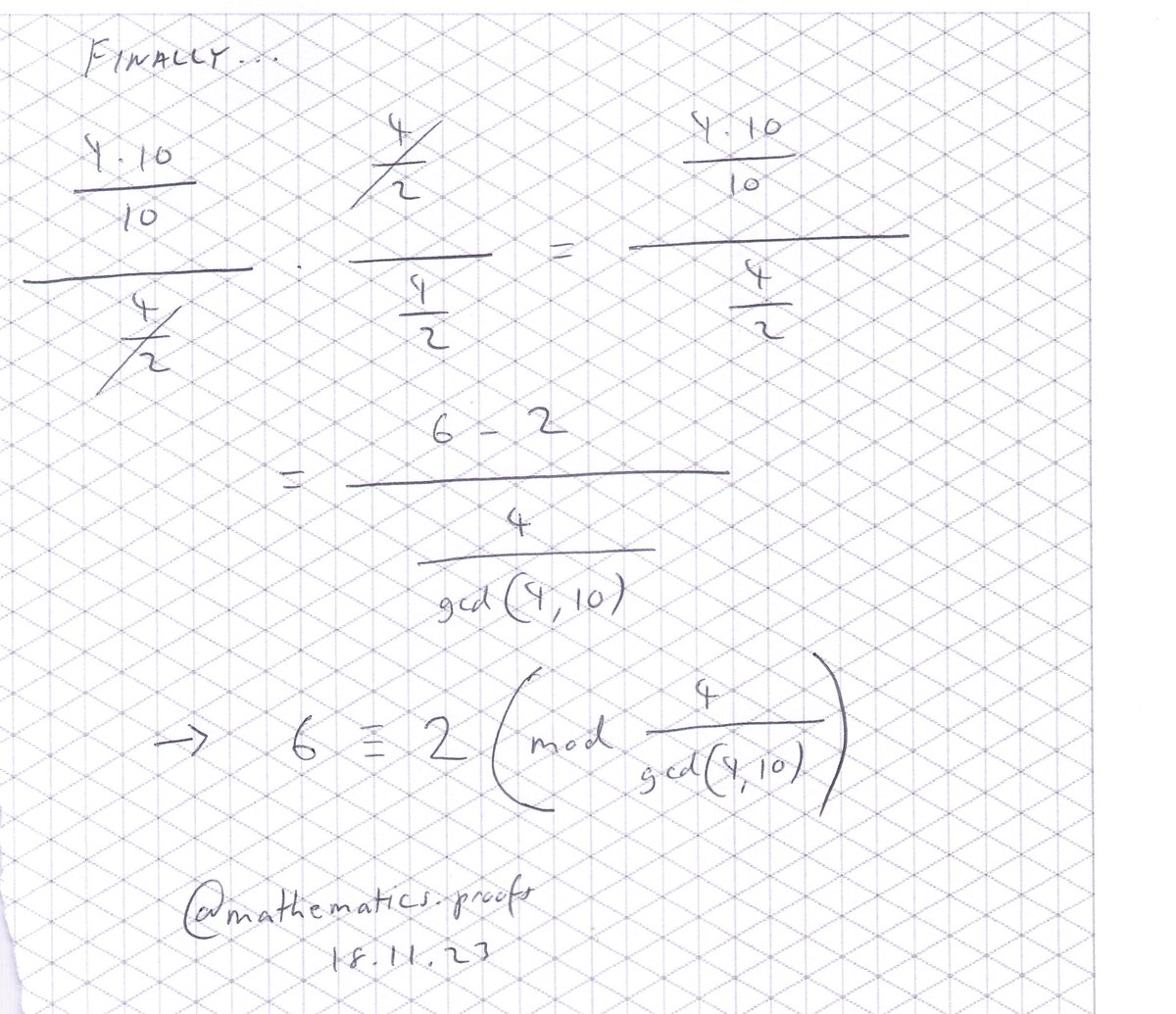
Okay, last one of the day (I promise 🤣), a kind of exhibition problem... Show that 2²⁰+3³⁰+4⁴⁰+5⁵⁰+6⁶⁰ is divisible by 7. #furtherpuremaths #modularcongruence #modulararithmetic #clockarithmetic
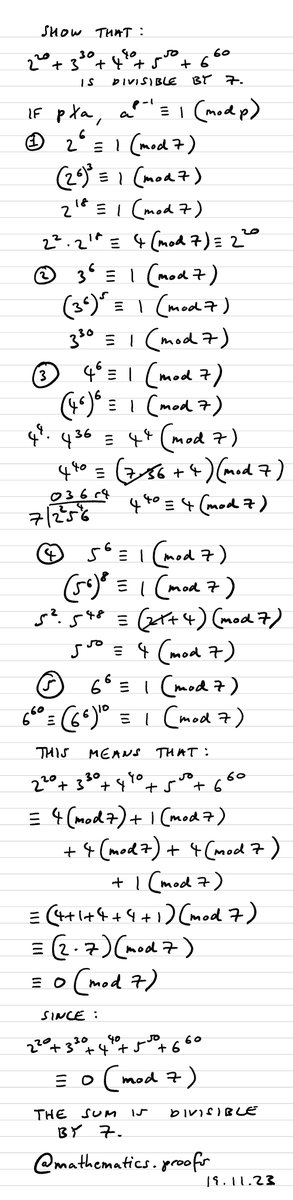
Let (G, *) be a finite group. Prove that every element in G must have finite order. *With extra workings for comprehension of the proof. #furtherpuremaths #grouptheory #modulararithmetic


Tip: Keep on writing the definitions of notation you haven't internalised yet. Once those definitions have been internalised, do the same for new / more advanced notation. Keep going. At the end of the day, maths is a language as well. #modulararithmetic #maths

Could this be a basic 4 dimensional universe? Here come the experiments... #modulararithmetic #math #mathematics

The properties of groups give rise to corresponding properties of #CayleyTables. *Extended Notes and Workings #furtherpuremaths #modulararithmetic #modularcongruence

Solve the congruence equation 42y ≡ 168 (mod 35). *Full workings and explanation included. #furtherpuremaths #modularcongruence #modulararithmetic #clockarithmetic
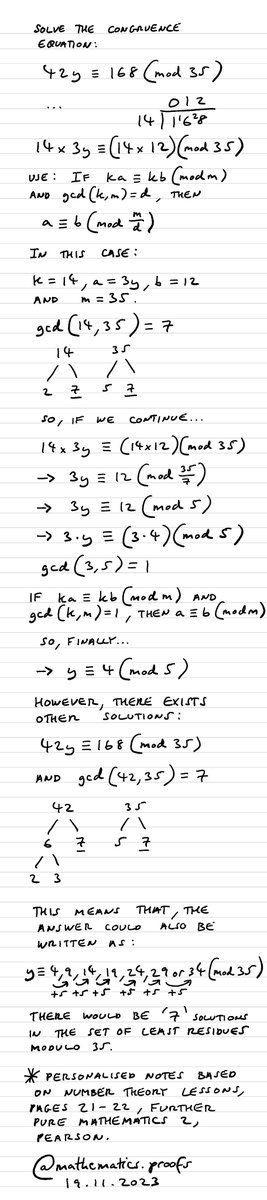
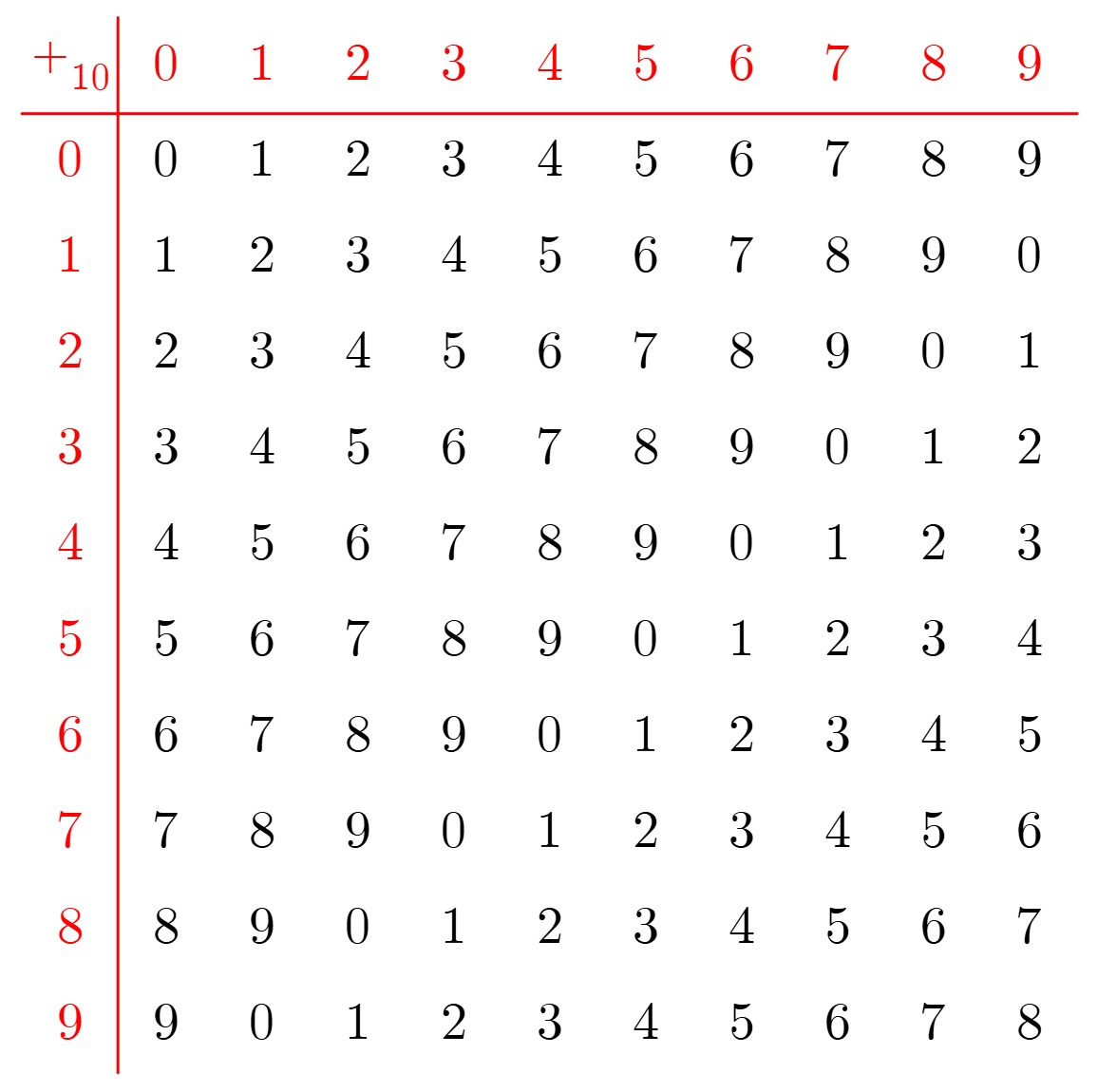
Cyclic Groups: Cayley table for the group (ℤ₁₀, +). Is there closure? Can you spot the identity element? Can you spot the inverses? #cayleytables #cyclicgroups #modulararithmetic #furtherpuremaths
Visualising university mathematics: Cosets of the subgroup 3Z in Z. Tip: If you can't understand a larger problem, break it down into a smaller problem. Perform smaller simulations. This is the secret to clarity in maths. #abstractalgebra #laraalcock #modulararithmetic

The set {1, 3, 5, 7} forms a group under multiplication modulo 8. Show that this group is not cyclic. *With extra notes and workings. #modulararithmetic #cyclicgroups #clockarithmetic #furtherpuremaths
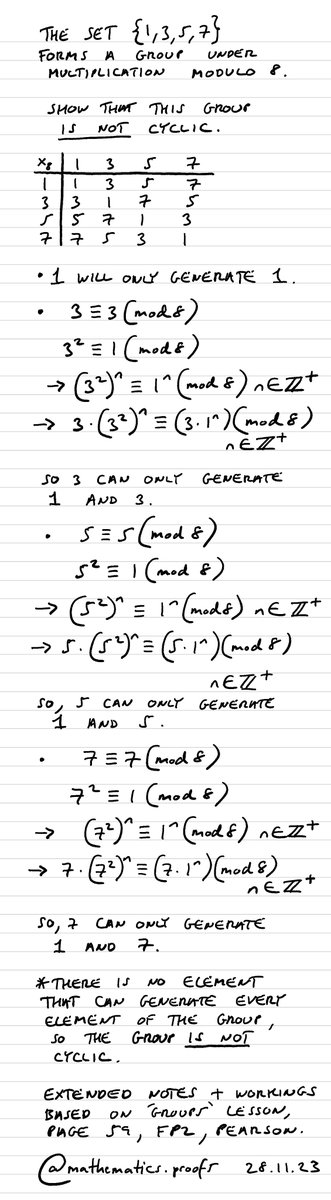
Each mod has a world of its own... When you're in (mod11) you're in (mod11). Don't ask questions, just solve. 😆 If 4x¹¹≡ 3 (mod 11), then x ≡ 9 (mod 11). #furtherpuremaths #modularcongruence #modulararithmetic #clockarithmetic

Something went wrong.
Something went wrong.
United States Trends
- 1. Arsenal 302K posts
- 2. Russ 29.8K posts
- 3. Martinelli 33K posts
- 4. White House 479K posts
- 5. Lakers 39.4K posts
- 6. NASA 72.1K posts
- 7. Atlas 60.8K posts
- 8. Crosby 8,616 posts
- 9. Atletico 116K posts
- 10. Simeone 22.7K posts
- 11. #COYG 6,488 posts
- 12. Platner 10.8K posts
- 13. Warriors 56.2K posts
- 14. Gyokeres 42.2K posts
- 15. John Brennan 28.5K posts
- 16. Woody Johnson 2,617 posts
- 17. Napoli 31.6K posts
- 18. Rashford 66.6K posts
- 19. $BYND 153K posts
- 20. #ARSATM 6,691 posts