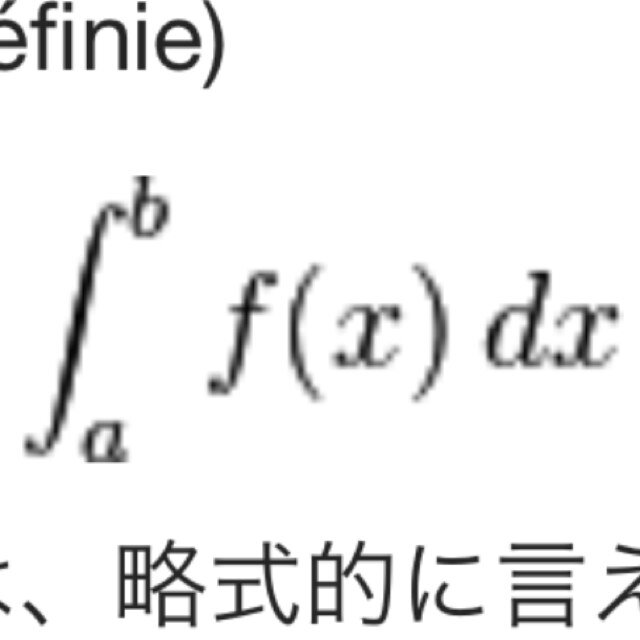2つの独立した三角形ABCとA'B'C'があり、BC=a、CA=b、AB=c、B'C'=a'、C'A'=b'、A'B'=c'とする。△ABC、△A'B'C'の内接円の半径をそれぞれr、r'とする時、 36rr'≦aa'+bb'+cc' となることを証明せよ。
トロコイドx=a(θ-k sinθ),y=a(1-k cosθ)は、θを消去してxとyだけの式に直せるか。(aとkは実数定数)
2つの独立した三角形ABCとA'B'C'があり、BC=a、CA=b、AB=c、B'C'=a'、C'A'=b'、A'B'=c'とする。△ABC、△A'B'C'の内接円の半径をそれぞれr、r'とする時、 36rr'≦aa'+bb'+cc' となることを証明せよ。
トロコイドx=a(θ-k sinθ),y=a(1-k cosθ)は、θを消去してxとyだけの式に直せるか。(aとkは実数定数)
2つの独立した三角形ABCとA'B'C'があり、BC=a、CA=b、AB=c、B'C'=a'、C'A'=b'、A'B'=c'とする。△ABC、△A'B'C'の内接円の半径をそれぞれr、r'とする時、 36rr'≦aa'+bb'+cc' となることを証明せよ。
トロコイドx=a(θ-k sinθ),y=a(1-k cosθ)は、θを消去してxとyだけの式に直せるか。(aとkは実数定数)
2つの独立した三角形ABCとA'B'C'があり、BC=a、CA=b、AB=c、B'C'=a'、C'A'=b'、A'B'=c'とする。△ABC、△A'B'C'の内接円の半径をそれぞれr、r'とする時、 36rr'≦aa'+bb'+cc' となることを証明せよ。
United States 趨勢
- 1. #DMDCHARITY2025 613K posts
- 2. #TusksUp N/A
- 3. #AEWDynamite 20.8K posts
- 4. #TheChallenge41 2,203 posts
- 5. Ryan Leonard N/A
- 6. #Survivor49 2,878 posts
- 7. Skyy Clark N/A
- 8. Diddy 75.9K posts
- 9. Jamal Murray 7,162 posts
- 10. Claudio 29.9K posts
- 11. Yeremi N/A
- 12. Steve Cropper 6,302 posts
- 13. seokjin 154K posts
- 14. Earl Campbell 2,188 posts
- 15. Hannes Steinbach N/A
- 16. Free Tina 13.4K posts
- 17. Klingberg N/A
- 18. Monkey Wards N/A
- 19. Milo 12.6K posts
- 20. Hilux 6,620 posts
Loading...
Something went wrong.
Something went wrong.