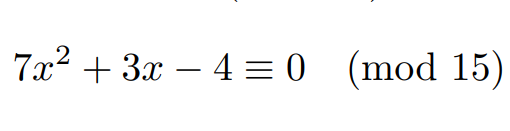#modulararithmetic search results
Finding the remainder | Give it a try? youtube.com/watch?v=9Y6Wt2… #sharingisthenewlearning #modulararithmetic

Modular Arithmetic "mod" is known as the operator of Modular Arithmetic Given (a)mod(b)=c where a,b,c are integers(±z). Where a is the dividend, b is the divisor, and c is the remainder. #sharingisthenewlearning #mod #modulararithmetic
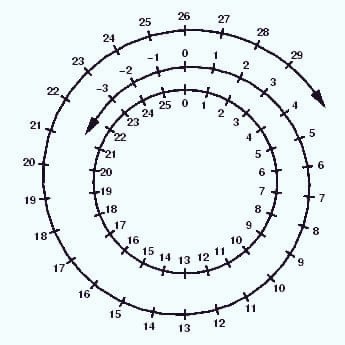
🔢 LeetCode Daily: Smallest Missing Integer ✅ Modular arithmetic magic! Track remainder frequencies, consume greedily from 0 upward. ⚡ O(n) with mod tracking 🎯 Remainder classes = equivalence 💡 Handle negatives: ((n%v)+v)%v #LeetCode #CPlusPlus #ModularArithmetic

Let (G, *) be a finite group. Prove that every element in G must have finite order. *With extra workings for comprehension of the proof. #furtherpuremaths #grouptheory #modulararithmetic


#POTD #Math #ModularArithmetic #Tougher Problem of the Day! Here's a weird one today. Clearly we would never say that 7 = i. However, did you know that 7 is congruent to i, mod 10? That is: 7 ≡₁₀ i. Nice!

Solved LeetCode's “Count the Number of Arrays with K Matching Adjacent Elements”! 🎯 Applied combinatorics: 🧮 C(n-1, k) × m × (m-1)^(n-k-1) ⚙️ Used fast mod inverse & exponentiation ✅ Great practice for math-based problems! #LeetCode #CodingChallenge #ModularArithmetic
Modular Arithmetic: Studying the nature of the cyclical group ({0, 1, 2, 3, 4}, addition modulo 5). Properties of a Group: Closure ✅ Identity ✅ Inverses ✅ Associativity ✅ #modulararithmetic #furtherpuremaths

#POTD #Math #ModularArithmetic Problem of the Weekend! Here's the last in the series this week. You'll need to put on your thinking caps for at least one part, if not two. There are also (at least) two good ways to attack this one. Have fun!
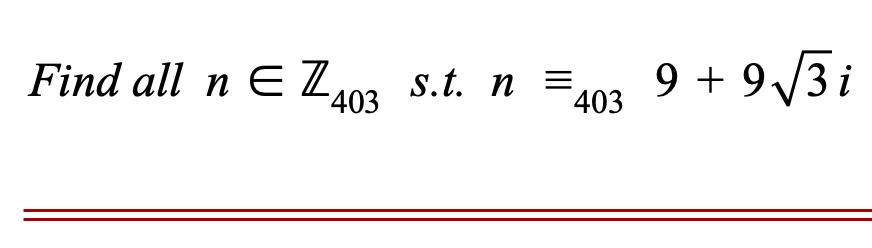
Tip: Keep on writing the definitions of notation you haven't internalised yet. Once those definitions have been internalised, do the same for new / more advanced notation. Keep going. At the end of the day, maths is a language as well. #modulararithmetic #maths

#POTD #Math #ModularArithmetic Problem of the Day! Here's the followup modular arithmetic problem to yesterday's. If you're not already familiar with these, it's time to get your learn on! Extra Hint: there are more than two answers!
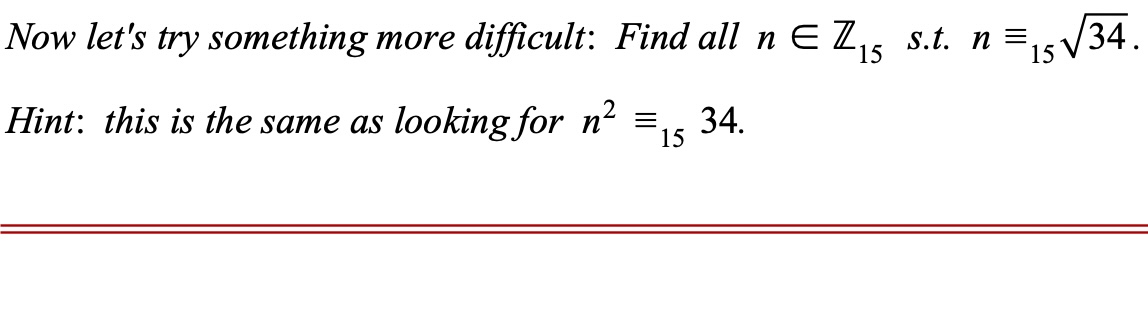
#POTD #Math #ModularArithmetic Problem of the Day! We've been building up to tomorrow's Problem of the Weekend, and today's should be a piece of cake if you were able to make it through yesterday's finding of n's congruent to 𝒊. (I've been looking for the best i: 𝒊? ⅈ? 𝖎?)
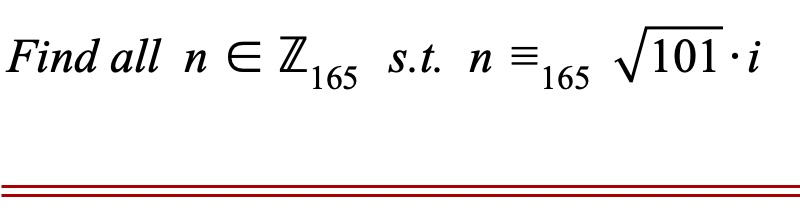
Problem of the Day #69: a ≡ 68 (mod 1967) a ≡ 69 (mod 1968) a ≡ ? (mod 14) Find the remainder of a divided by 14. The solution link is in the bio. #ModularArithmetic #NumberTheory #RemainderProblem #ProblemSolving #ExactScience

🔢 LeetCode Daily: Smallest Missing Integer ✅ Modular arithmetic magic! Track remainder frequencies, consume greedily from 0 upward. ⚡ O(n) with mod tracking 🎯 Remainder classes = equivalence 💡 Handle negatives: ((n%v)+v)%v #LeetCode #CPlusPlus #ModularArithmetic

Finding the remainder | Give it a try? youtube.com/watch?v=9Y6Wt2… #sharingisthenewlearning #modulararithmetic

Modular Arithmetic "mod" is known as the operator of Modular Arithmetic Given (a)mod(b)=c where a,b,c are integers(±z). Where a is the dividend, b is the divisor, and c is the remainder. #sharingisthenewlearning #mod #modulararithmetic

Find the remainder when 2¹⁰⁰⁰ is divided by 13. *Full workings. #furtherpuremaths #modulararithmetic #fermatslittletheorem #alevelmaths
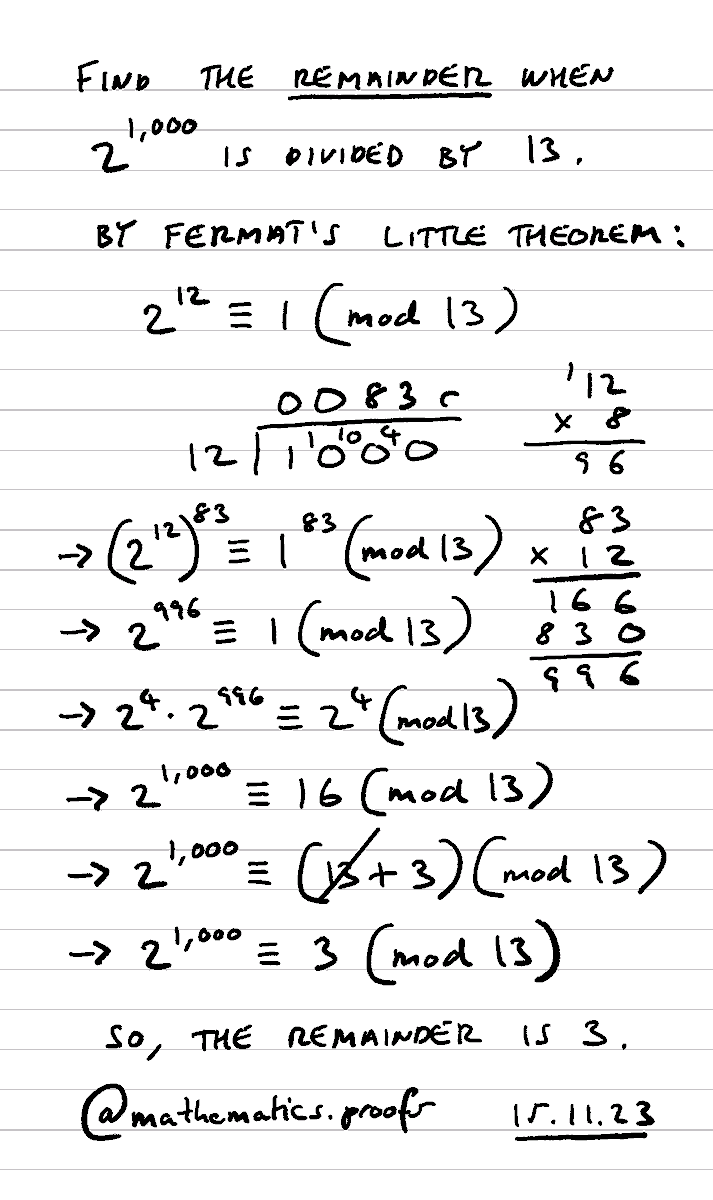
Prove that 5²² + 17²² ≡ 6 (mod 11) #furtherpuremaths #modularcongruence #modulararithmetic #fermatslittletheorem
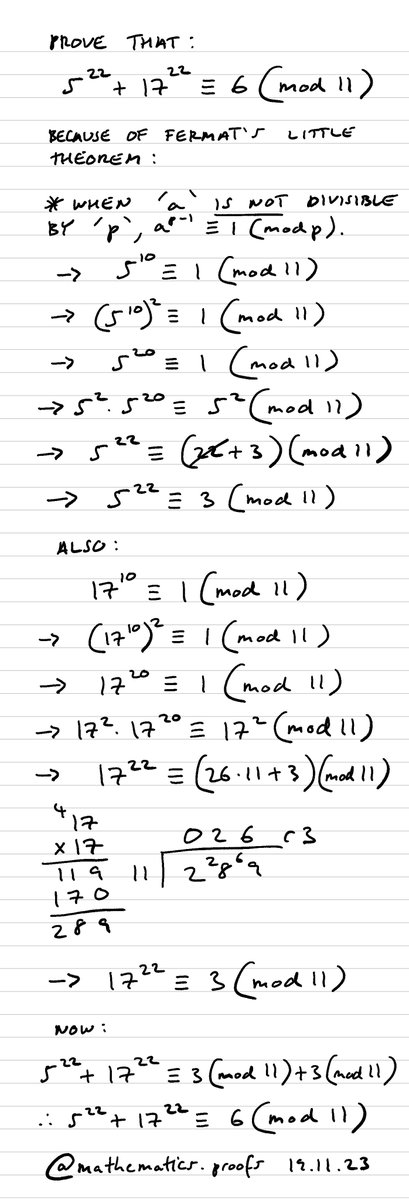
Find the least residue of 3²⁰² modulo 11. #furtherpuremaths #modulararithmetic #fermatslittletheorem #clockarithmetic

Let (G, *) be a finite group. Prove that every element in G must have finite order. *With extra workings for comprehension of the proof. #furtherpuremaths #grouptheory #modulararithmetic


(2 Ways) Solve the congruence equation: 75x≡12(mod237) #modularcongruence #modulararithmetic #alevelmaths #furtherpuremaths
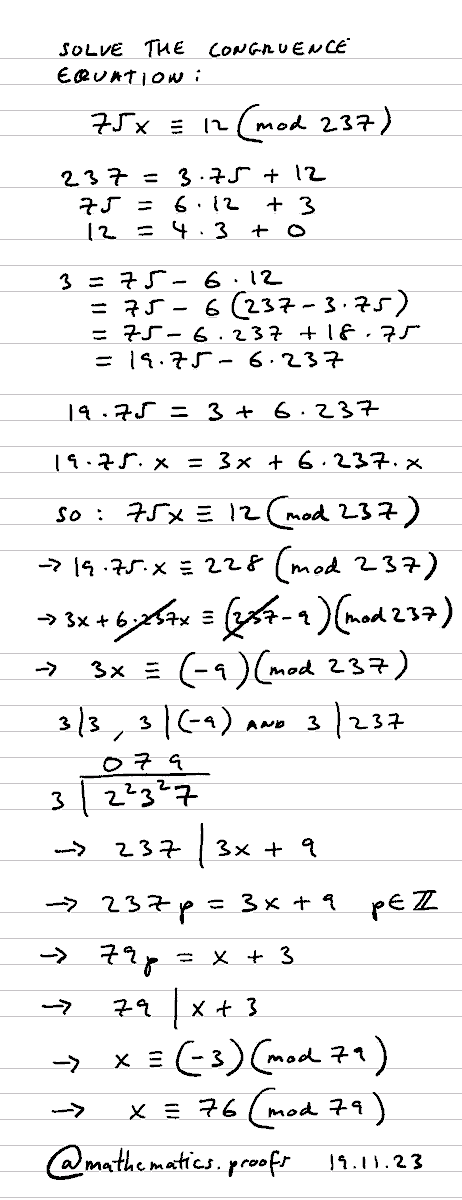

🔢 LeetCode Daily: Smallest Missing Integer ✅ Modular arithmetic magic! Track remainder frequencies, consume greedily from 0 upward. ⚡ O(n) with mod tracking 🎯 Remainder classes = equivalence 💡 Handle negatives: ((n%v)+v)%v #LeetCode #CPlusPlus #ModularArithmetic

Modular Arithmetic: Studying the nature of the cyclical group ({0, 1, 2, 3, 4}, addition modulo 5). Properties of a Group: Closure ✅ Identity ✅ Inverses ✅ Associativity ✅ #modulararithmetic #furtherpuremaths

Tip: Keep on writing the definitions of notation you haven't internalised yet. Once those definitions have been internalised, do the same for new / more advanced notation. Keep going. At the end of the day, maths is a language as well. #modulararithmetic #maths

Resolving the division anomaly. *Work with integers included. #furtherpuremaths #modularcongruence #modulararithmetic #alevelmaths


Okay, last one of the day (I promise 🤣), a kind of exhibition problem... Show that 2²⁰+3³⁰+4⁴⁰+5⁵⁰+6⁶⁰ is divisible by 7. #furtherpuremaths #modularcongruence #modulararithmetic #clockarithmetic
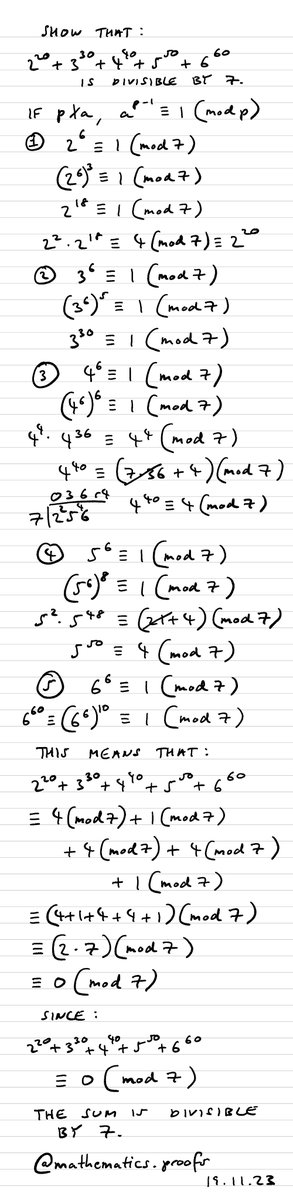
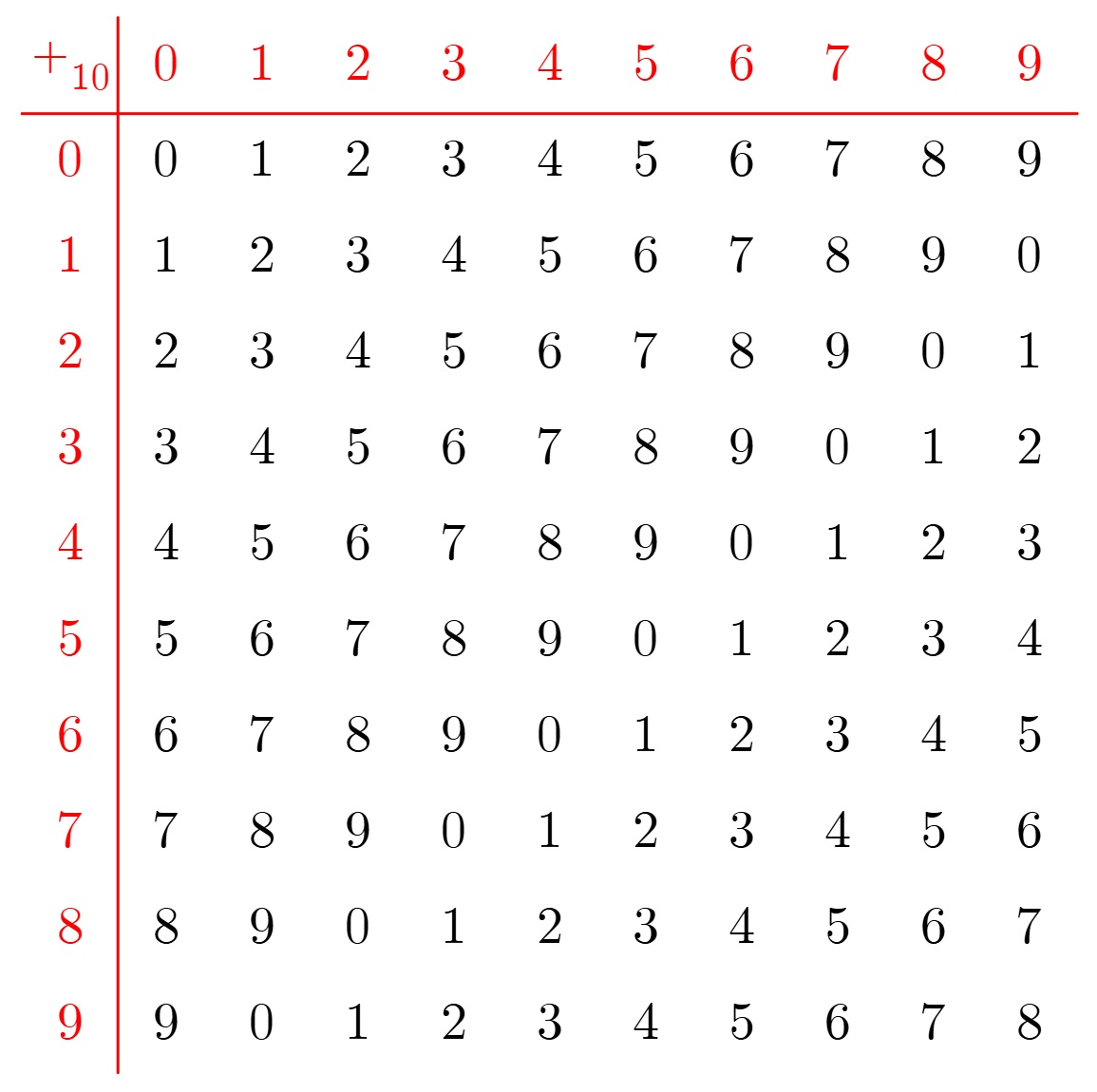
Cyclic Groups: Cayley table for the group (ℤ₁₀, +). Is there closure? Can you spot the identity element? Can you spot the inverses? #cayleytables #cyclicgroups #modulararithmetic #furtherpuremaths
Could this be a basic 4 dimensional universe? Here come the experiments... #modulararithmetic #math #mathematics

The properties of groups give rise to corresponding properties of #CayleyTables. *Extended Notes and Workings #furtherpuremaths #modulararithmetic #modularcongruence

Solve the congruence equation 42y ≡ 168 (mod 35). *Full workings and explanation included. #furtherpuremaths #modularcongruence #modulararithmetic #clockarithmetic
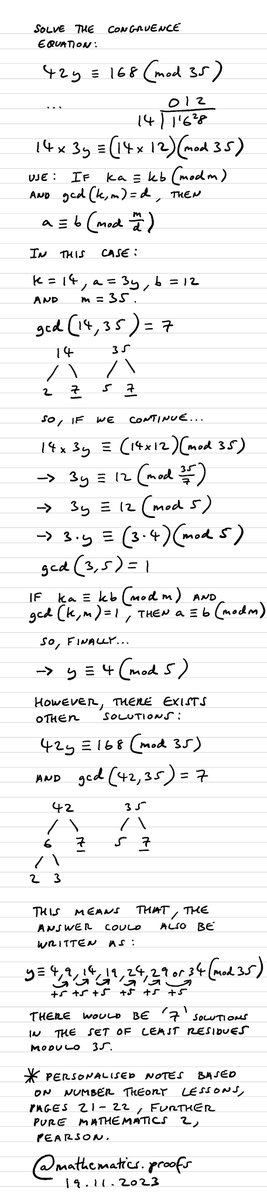
Visualising university mathematics: Cosets of the subgroup 3Z in Z. Tip: If you can't understand a larger problem, break it down into a smaller problem. Perform smaller simulations. This is the secret to clarity in maths. #abstractalgebra #laraalcock #modulararithmetic

The set {1, 3, 5, 7} forms a group under multiplication modulo 8. Show that this group is not cyclic. *With extra notes and workings. #modulararithmetic #cyclicgroups #clockarithmetic #furtherpuremaths
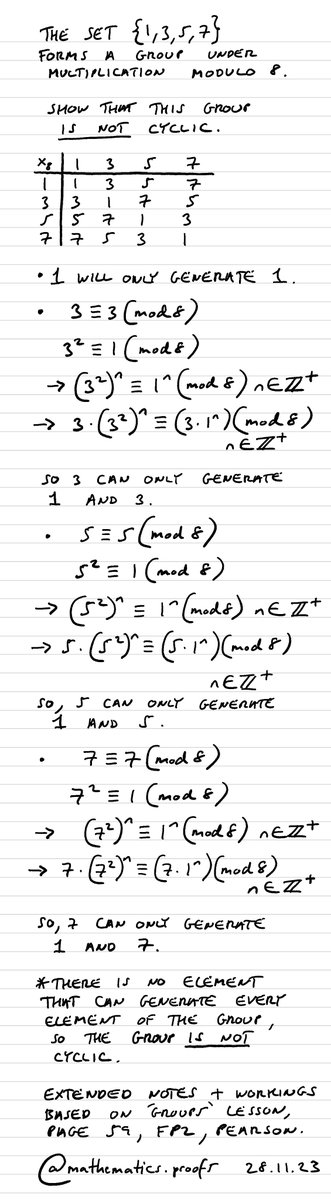
Something went wrong.
Something went wrong.
United States Trends
- 1. Austin Reaves 28K posts
- 2. #LakeShow 2,413 posts
- 3. Trey Yesavage 34.2K posts
- 4. Jake LaRavia 3,818 posts
- 5. Blue Jays 59.9K posts
- 6. #LoveIsBlind 3,982 posts
- 7. jungwoo 90K posts
- 8. #AEWDynamite 22.1K posts
- 9. doyoung 71.7K posts
- 10. Rudy Gobert N/A
- 11. Snell 13.3K posts
- 12. #Lakers N/A
- 13. Pelicans 4,113 posts
- 14. Anthony Davis 3,987 posts
- 15. #WorldSeries 66K posts
- 16. Kacie 1,687 posts
- 17. Wolves 61.6K posts
- 18. Happy Birthday Kat N/A
- 19. Bulls 26.3K posts
- 20. Dwight Powell N/A