English
English Indonesia Türkçe Deutsch Español Português Pусский Français Italiano Nederlands Polski العربية ไทย Tiếng Việt 繁體中文 简体中文 日本語 한국어
WKMathOrgGen's profile picture. 専門は数論. 博士(理学).『偉大な定理に迫る！理系脳を鍛える数学クイズ』『高校数学 至極の有名問題 240—文理対応・国公立大～難関大レベル』好評発売中.

有名問題・定理から学ぶ数学｜廣津孝

@WKMathOrgGen

専門は数論. 博士(理学).『偉大な定理に迫る！理系脳を鍛える数学クイズ』『高校数学 至極の有名問題 240—文理対応・国公立大～難関大レベル』好評発売中.

34Posts 64Followers 46Following
Pinned
WKMathOrgGen's profile picture.
有名問題・定理から学ぶ数学｜廣津孝
@WKMathOrgGen
Jun 24

『基礎からの「ガロア理論」』が本日6月24日発売になりました. 書店で見かけたらお手に取っていただければ幸いです. ちなみに, 一般書・実用書に分類されているショップもあるようですが, 読み物ではなく, 主定理まで証明の省略は原則なしの, 専門書と言って良い内容の数学書です.…

WKMathOrgGen's tweet image. 『基礎からの「ガロア理論」』が本日6月24日発売になりました. 書店で見かけたらお手に取っていただければ幸いです. ちなみに, 一般書・実用書に分類されているショップもあるようですが, 読み物ではなく, 主定理まで証明の省略は原則なしの, 専門書と言って良い内容の数学書です.…
0
0
9
1
1K
WKMathOrgGen's profile picture.
有名問題・定理から学ぶ数学｜廣津孝
@WKMathOrgGen
Oct 27

『基礎からの「ガロア理論」』初版第1刷(日本能率協会マネジメントセンター刊)において誤りがございました. 正誤表(2025年10月21日現在)は以下のリンクからご覧になれます. jmam.co.jp/pub/additional… 訂正してお詫びいたします.

0
0
2
1
46
WKMathOrgGen's profile picture.
有名問題・定理から学ぶ数学｜廣津孝
@WKMathOrgGen
Jan 7

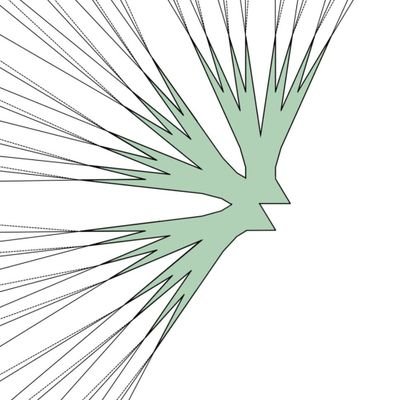
新理論「ミニチュア理論」に関する論文がarXivで公開されました. 格子ポリトープPの「平均大のミニチュア」とは何かを有理格子, 数え上げ, 平均値の極限を利用して定式化しました.…

0
0
3
0
212
WKMathOrgGen's profile picture.
有名問題・定理から学ぶ数学｜廣津孝
@WKMathOrgGen
Dec 17

日曜数学Advent Calendar 2024の18日目の記事『ミニチュア理論(格子点の幾何学)』をホームページで公開しました. wkmath.org/adv-2024-f.html 素朴ですが, 格子を利用すると, 凸体(格子点を頂点とするもの)の「平均大・標準大のミニチュア」が定式化できるという内容で, 正方形,…

WKMathOrgGen's tweet image. 日曜数学Advent Calendar 2024の18日目の記事『ミニチュア理論(格子点の幾何学)』をホームページで公開しました. wkmath.org/adv-2024-f.html 素朴ですが, 格子を利用すると, 凸体(格子点を頂点とするもの)の「平均大・標準大のミニチュア」が定式化できるという内容で, 正方形,…
0
1
12
1
1K
WKMathOrgGen's profile picture.
有名問題・定理から学ぶ数学｜廣津孝
@WKMathOrgGen
Oct 23, 2024

52個目のメルセンヌ素数2¹³⁶²⁷⁹⁸⁴¹-1(4102万4320桁)が発見され, 最大の素数の記録が更新されたそうです(52番目のメルセンヌ素数であるかどうかは未確定). 偶数の完全数とメルセンヌ素数の1対1対応と, 奇数の完全数が発見されていないことから, これは52個目の完全数の発見を意味します.

0
0
4
0
259
WKMathOrgGen's profile picture.
有名問題・定理から学ぶ数学｜廣津孝
@WKMathOrgGen
Jun 20, 2024

ガロア理論の書籍刊行に先立って, ホームページの「数学一般」の群論, 環論, 体論の各項目を順次更新しています. wkmath.org/gen.html ぜひご活用ください.

0
1
5
0
254
WKMathOrgGen's profile picture.
有名問題・定理から学ぶ数学｜廣津孝
@WKMathOrgGen
May 2, 2024

aが可逆であるとき, aの-n乗(n: 正の整数)は a⁻ⁿ=(a⁻¹)ⁿ …[1] と定義する方がベターです. a⁻ⁿ=(aⁿ)⁻¹ …[2] を定義とする本もありますが(高校の教科書など), aⁿの可逆性は完全に自明とは言えないため, [1]を定義とし, aⁿが可逆で(aⁿ)⁻¹=(a⁻¹)ⁿであることを示す方が理にかなっています.

0
0
2
0
210
WKMathOrgGen's profile picture.
有名問題・定理から学ぶ数学｜廣津孝
@WKMathOrgGen
Mar 22, 2024

偶完全数のちょっとした組合せ論的解釈を考案し, それをもとにクイズを作ってみました. 一般に, メルセンヌ素数2ᵖ-1に対して, 2ᵖ⁻¹×(2ᵖ-1)マスの方眼紙を罫線に沿って合同な小長方形に分割するとき, 分割の方法すべてにわたる小長方形の個数の総和はマス目の個数の2倍に等しくなります.

WKMathOrgHS's profile picture. 問題設定・数値設定の動機が明確で素朴な高校数学の問題―古典的な問題, 重要な定理・深い理論的背景に基づいた問題から, 応用面で重要な問題まで. 関連書籍『高校数学至極の有名問題 240: 文理対応・国公立大～難関大レベル』『偉大な定理に迫る！理系脳を鍛える数学クイズ』好評発売中. 毎週(月)問題, (金)クイズ配信.
有名問題・定理から学ぶ高校数学
 @WKMathOrgHS
Mar 22, 2024

今週のクイズ:《完全数》 p, qを素数とする. p×qマスの余白のない方眼紙を罫線に沿って1個以上の合同な小長方形に分ける. このような分け方すべてにわたる小長方形の個数の総和がマス目の個数の2倍に等しいとき, pqの値はいくらか. wkmath.org/arith-qz.html#… 答えはあの有名な整数です. #数学クイズ

0
0
2
1
528
0
0
2
0
339
WKMathOrgGen's profile picture.
有名問題・定理から学ぶ数学｜廣津孝
@WKMathOrgGen
Feb 28, 2024

整数論と組合せ論(と測度論?)の狭間で, 非常に素朴で興味深い問題を発見しました. 3平方和定理, 4平方和定理も活躍するのではないかとにらんでいます. 本の執筆が落ち着いたら, こちらも本格的な研究に入りたいと思います.

0
0
1
0
255
WKMathOrgGen's profile picture.
有名問題・定理から学ぶ数学｜廣津孝
@WKMathOrgGen
Feb 1, 2024

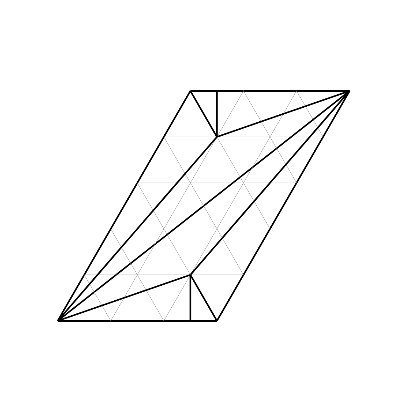
ちなみに, 平面がn個の三角形の周で分割されてできる領域の個数の最大値は3n²-3n+2であることが知られています(OEIS: A077588). wkmath.org/tbl-m.html#m-t… しかし, 空間がn個の四面体の面で分割されてできる領域の個数の最大値は『オンライン整数列大辞典』に載っていないようです.

0
0
1
0
263
WKMathOrgGen's profile picture.
有名問題・定理から学ぶ数学｜廣津孝
@WKMathOrgGen
Jan 31, 2024

ホームページで数表(添付画像はその一部) wkmath.org/tbl-m.html をまとめていると, 興味深い問題によく出会います. 空間がn個の楕円面(大きさは問わない)で分割されてできる領域の個数の最大値はいくらでしょうか. 『オンライン整数列大辞典』では見つけられませんでした.

WKMathOrgGen's tweet image. ホームページで数表(添付画像はその一部) wkmath.org/tbl-m.html をまとめていると, 興味深い問題によく出会います. 空間がn個の楕円面(大きさは問わない)で分割されてできる領域の個数の最大値はいくらでしょうか. 『オンライン整数列大辞典』では見つけられませんでした.
0
0
1
0
175
J_Koizumi_233's profile picture. 数学を研究しています。

J. K.

@J_Koizumi_233
musubimeriron's profile picture. Professor of Knot Theory

musubimeriron

@musubimeriron
t88897937768's profile picture. 数学科M2/都数, 数研, 数物セミナーAdvanced常連/数論力学系(arithmetic dynamics), 代数的整数論(algebraic number theory), 楕円曲線(elliptic curves)/t888は言いにくいのでt8(てぃーはち)って呼んで下さい

t888

@t88897937768
gunron_tan's profile picture. #群論 に入門できる連ツイを毎日投稿。最も基礎・初歩の部分から、かなりていねいに解説。①#群論の初歩→②#代数系の初歩→③#巡回群とは→④#群論入門_正規部分群編→(この先は固定ツイに記載) ※群論以外の数学全般もつぶやきます。※#群馬県 の事もつぶやきます。※#群馬県は群論と関係ありません ※アイコンは群馬県です。

群論たん (※大学の代数学の入門用学術たん・抽象代数学たん)

@gunron_tan
ikahakatsu's profile picture. 整数大好きZ世代！！

katsu

@ikahakatsu
Esquisse1102's profile picture. 雑食です

えすきす

@Esquisse1102
alytile's profile picture. 日本テセレーションデザイン協会 代表 ミラクル エッシャー展 スーパーバイザー/ニュートン別冊 図形編 エッシャー記事監修/ 映画「エッシャー 視覚の魔術師」広報翻訳協力/ マーブルシュッド 「Tessellation」監修 / 著書 「M.C.エッシャーと楽しむ算数・数学パズル」「ペンローズの幾何学」

Yoshiaki Araki 荒木義明

@alytile
1806_04679's profile picture. 積んだ徳からカルマを引いたら最期に閻魔と笑えるか？

味覚クリティカル

@1806_04679
espresso3141592's profile picture. 数学ビギナー ☕️ IT会社員 #赤雪江 #松坂集合位相 #石井線形代数 #黒田微分積分

caffeine

@espresso3141592
ginga_no_hoshi's profile picture. ピアノ・琵琶練習🎹絵の練習✏️数学・科学🪐数学・科学と芸術の狭間の部分を探究していきたいです。「科学と芸術は同じ方向へいく」(byコクトー)自然・動物福祉🍀放送大学・哲学塾カントで勉強中📖

ギンガノホシ

@ginga_no_hoshi
Tomuo2000's profile picture. 数学者📺笑わない数学(NHK総合)監修 📺数学者は宇宙をつなげるか～abc予想をめぐる数奇な物語📺素数の魔力に囚われた人々～リーマン予想📖「数学をする」ってどういうこと?(技術評論社)📖日本一わかりやすいABC予想(ビジネス教育出版)📖 数学の力〜高校数学で読みとくリーマン予想（日経サイエンス社）

小山信也

@Tomuo2000
m_2sei's profile picture. ひとりごとです。素数大富豪は人を幸せにするゲームだと思ってます。フォローとかしなくていいよ！

二世

@m_2sei
atsushifujioka's profile picture. 関西大学システム理工学部数学科

藤岡敦

@atsushifujioka
ft5EFFg4jRlCOEm's profile picture. 旧帝大数学科出身　数学の博士号持ってます

数学科のつぶやき

@ft5EFFg4jRlCOEm
GyodaYasuaki's profile picture. 名古屋大学高等研究院/大学院多元数理科学研究科、YLC特任助教。団代数の基礎とその応用に興味があります。二浪して院試にも落ちたことがありますが数学を続けています。

行田康晃/Yasuaki GYODA

@GyodaYasuaki
TomS04996946's profile picture. 「数学アートの部屋」（https://t.co/KgbX0bC9Gc）では数学を使って描ける美しいアートをその描き方とともに紹介しています。このサイトの新着情報や更新情報などをお伝えします。当サイトの各種数学アートについての質問、コメントはDMやリプライでお願いします。

数学アートの部屋

@TomS04996946
GU_Takaesu's profile picture. 群馬大学 共同教育部 数学専攻 教授 / 数理物理

高江洲 俊光

@GU_Takaesu
elmoboss's profile picture. 広島人です。ぼちぼちつぶやきます。

えるもー

@elmoboss
ron1827's profile picture. 四十路半ば。数学・特撮・将棋など好き。妻と２男児（５歳、１歳）。「笑わない数学」ライター／数学カフェ @mathcafe_japan など。数学のお仕事・ご依頼募集中（相談はDMまで）匿名のご質問は https://t.co/QLsY50SEEH へどうぞ。amazonアソシエイト参加中

龍孫江（りゅうそんこう）数学YouTuber／お仕事依頼歓迎して〼

@ron1827
buku_t's profile picture. 数学とゲームが好きな研究者 | じょきょー | 著書『組合せゲーム理論の世界』 | GU←NII (←ITF←TUS) | N高グループ研究部(#KdEi研) | 数理空間トポス | エルデシュ数3 | https://t.co/HAa3bIQT3s | @Modern_Math | アイコン:ことり野デス子さん

ぶく

@buku_t
gakuikeda1109's profile picture. 【ディンキン数学研究室】趣味はチェロの演奏. 料理も好き. #行列と行列式の基礎 #テンソル代数と表現論 #数え上げ幾何学講義 次作は #リー環とディンキン数学 （仮題）と #初等ガロワ理論 と #正標数の可換環論 (共著)

池田 岳

@gakuikeda1109
mathraphsody's profile picture. 数学・表現論・リー群とリー環，著書：フリーズの数学 スケッチ帖・多項式のラプソディー・代数群と軌道・幾何学と不変量・射影幾何学の考え方，フォロワーは相互フォローできる人のみ．原則鍵垢不可． Representation Theory, Lie Groups & Lie algebras, Frieze Patterns

lestroarmonico

@mathraphsody
yutkatkitkat's profile picture. 数学が好きです。 特に関数解析学が好きです。 Mathpediaの解析分野のライター（執筆した記事群は「関数解析の基礎」）です。 大学数学（解析入門、位相、線形代数、測度論、関数解析など）、高校数学のオンライン家庭教師をしています。ご依頼はDMでお願いします。 原田病に罹り治療中。

Yuta Kataoka（片岡）

@yutkatkitkat
sakGrothendieck's profile picture. 大阪大学院数学専攻M1 非可換代数幾何学

さく

@sakGrothendieck
sshimo_'s profile picture. 数学の研究をしたくなったので，退職して院進しました．専門は距離空間上のgradient flowです．東大数理D2．ツイートは個人の見解です．

s.shimo

@sshimo_
waku2mathtalk's profile picture. 数学が苦手な人にもわかりやすい大学の数学の話をpodcastやyoutubeで放送しています。

ワクワク数学トーク

@waku2mathtalk
FumiharuKato's profile picture. ZEN大学教授 東京工業大学名誉教授 株式会社SCIENTA・NOVA代表取締役 ZEN数学センター（ZMC）所長 数研出版高校教科書「数学シリーズ」著者 NPO法人数理の翼顧問 数理空間トポス顧問

Fumiharu Kato 加藤文元（Bungen）

@FumiharuKato
apu_yokai's profile picture. かつての「妖怪テーマパーク」の管狸人 。今は経理関係の仕事をしている。平日は通勤電車の中で数学で遊ぶ。数学は仕事と全く関係ない、完全な趣味である。 「ゆる数学」ブログはじめました!（更新遅め）😃

ａｐｕ

@apu_yokai
ysk8128's profile picture. 数学,物理教えてます🧑‍💻日々探求ᝰ✍🏻

徳島のとある塾講師

@ysk8128
Kiwamu_Watanabe's profile picture. 中央大学理工。代数幾何。「すごすぎる数の図鑑」発売中：https://t.co/jpAeKfGmKz 数学YouTube：https://t.co/NfanAGVR0k 2018年度建部賢弘賞受賞

渡邉究/数学科准教授/KADOKAWAより「すごすぎる数の図鑑」発売中/YouTube

@Kiwamu_Watanabe
m_ishii13's profile picture. 研究者, テニス

Masahiro ISHII

@m_ishii13
math_honeyworks's profile picture. AW(アクセル・ワールド)のアニメ2期を延々と待ってる変人．数弱ですが，数学が好きです．す．よろしくお願いします．鹿島6章不完全性定理がよく分からず，素朴集合論の復習に逃亡中…

83

@math_honeyworks
integers_blog's profile picture. 数学者。准教授ではない。

【絶対査読】査読査読ゅ査読査読【絶対査読】

@integers_blog
Lucien0308's profile picture. 数学博士。数学の勉強を応援しています！／3児の父／クリスチャン／ブログやっています！(URLはWeb欄↓更新止まってます😅)／質問箱https://t.co/zxqn92VHQl

ルシアン

@Lucien0308
Kantaro196611's profile picture. YouTube チャンネル 鈴木貫太郎https://t.co/CGAsoM4WWyホームページhttps://t.co/yVWrIOxVa7 Amazonアソシエイトのリンクを使用しています

鈴木貫太郎

@Kantaro196611
Rodin_math's profile picture. どこかの大学のなんとか助教。研究分野は団代数（クラスター代数）。最近はマルコフ数を一般化して遊んでる。エルデシュ数は5（プレプリント込みで3）。2浪。アイコンとヘッダーは@fuku__hukuさんから頂きました。

ロダン@数学徒

@Rodin_math
rikoushonotana's profile picture. 書泉グランデ（神保町）公式アカウント 数学、物理学書担当がお勧めの商品や、フェア、数学、物理関連情報をつぶやきます。 『数学にはこんなマーベラスな役立て方や楽しみ方があるという話をあの人やこの人にディープに聞いてみた本2』（日本評論社）数学書担当掲載中 https://t.co/SrlvKyAZAU

書泉_MATH

@rikoushonotana
sugakubunka's profile picture. 株式会社すうがくぶんかは、#もっと社会に数学を をミッションに、社会人への数学/統計学/機械学習の普及活動や数学を一緒に学びあえる場の創生に取り組んでいます。現代数学レクチャーシリーズ #現数レク 、数学の祭典 #MathPower を主催しています。

すうがくぶんか

@sugakubunka
MurakamiMath's profile picture. 若手数学者。研究テーマは整数論、中でもモジュラー形式と結び目の関係。 面白いなと思った数学の話題や、自分の研究を紹介しています。

村上友哉

@MurakamiMath
pc3taro's profile picture. 過去に数学・教育等の関連事業を本業としていましたが、現在はYouTube・noteでの活動から、再度本業としたいと思っています。数学関係の仕事依頼はnoteの「仕事依頼」のページをご覧いただいたうえで、ご依頼願います。 【告知】鍵アカからのフォローは、私からのフォローバック承認前提にて認めます。

PC三太郎

@pc3taro
nichimath's profile picture. ５分間で数学を語るイベント「日曜数学会」の公式Twitterです。日曜数学会は年三回(2,6,10月)開催。日曜数学会のイベント情報や数学トピックスなどを呟きます。中の人は @kiguro_masanao ※数学の質問は受け付けておりません。ご了承ください。

日曜数学会

@nichimath
tsujimotter's profile picture. 札幌に住む情報系研究者です（札幌/つくば/横浜/札幌）。北海道情報大学 情報メディア学部 講師。本業の傍ら「日曜数学者」と名乗り数学の魅力を伝える活動をしています／ブログ→ https://t.co/HMaQx0lVJf／触れるゼータ関数／#日曜数学会 スタッフ／#マスパーティ

tsujimotter 日曜数学者

@tsujimotter
tatenoso's profile picture. このアカでは主に考案したカードゲーム「ゴールデンエッグラー」の普及活動をしています。普段は数学の研究をしています。専門は代数的整数論・岩澤理論で、ガロア理論やトポロジー等の抽象論が好きです。大学数学で質問のある人は一緒に考えるので送って下さい。TOEFL100点とる程英語もやったので留学したい人とか聞いて下さい。

T野

@tatenoso
AkiyaMath's profile picture. 数学を自由に楽しむ人｜修士（数理学）｜中高教諭専修免許（数学）｜数学検定１級｜統計検定１級を目指して勉強中です！現在：２級｜昨年度まで大学への数学の「学コン」を解いていました。来年度から復帰したい！｜「それぞれが抱える “好き” を大切に…。」｜管理サイト『数学の時間』↓

AkiyaMath 数学愛好家

@AkiyaMath
WKMathOrgHS's profile picture. 問題設定・数値設定の動機が明確で素朴な高校数学の問題―古典的な問題, 重要な定理・深い理論的背景に基づいた問題から, 応用面で重要な問題まで. 関連書籍『高校数学至極の有名問題 240: 文理対応・国公立大～難関大レベル』『偉大な定理に迫る！理系脳を鍛える数学クイズ』好評発売中. 毎週(月)問題, (金)クイズ配信.

有名問題・定理から学ぶ高校数学

@WKMathOrgHS

United States Trends

Something went wrong.


Something went wrong.