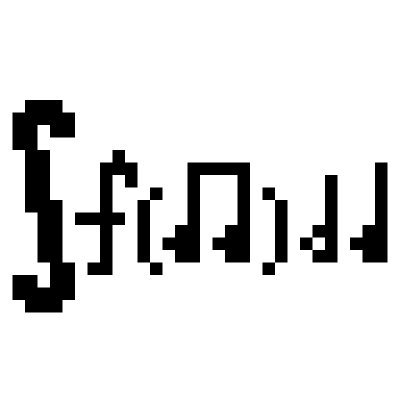You might like
ルベーグ積分の何が問題かというと、正の部分と負の部分に分けて定義されるせいで振動に弱くなること。だから有界区間でも「条件収束」する広義リーマン積分にすら負けることがある。ヘンストック・クルツヴァイル積分はその弱点を克服した上に単調収束定理や優収束定理の拡張も成り立つという優れ物。
ルベーグ可積分ではない(従ってリーマン可積分でもない)が、ヘンストック・クルツヴァイル可積分な関数の例。 ルベーグ積分は「万能」と言えるかもしれませんが、「全能」ではありません。


数学における研究課題の見つけ方 mathlog.info/articles/3589 #Mathlog 書いてみました.参考になるかどうかはわかりませんが,日々頑張っている学生の皆さんの一助となれば幸いです.
こんな式で全ての有理数が1回ずつ出てくるとな しかもカルキン・ウィルフ・ツリーの幅優先探索順に…!
Consider the function f(x) = 1 / ( ⌊x⌋ + 1 − {x} ) and the sequence of numbers 0, f(0), −f(0), f(f(0)), −f(f(0)), f(f(f(0))), −f(f(f(0))), ... Congratulations, you've just listed every rational number exactly once!

Consider the function f(x) = 1 / ( ⌊x⌋ + 1 − {x} ) and the sequence of numbers 0, f(0), −f(0), f(f(0)), −f(f(0)), f(f(f(0))), −f(f(f(0))), ... Congratulations, you've just listed every rational number exactly once!

新装版になって共立出版から出るらしい。 kyoritsu-pub.co.jp/book/b10018285…
kyoritsu-pub.co.jp
ベルヌーイ数とゼータ関数 新装版 - 共立出版
荒川 恒男 著
Q.279 ☆8 [2022新歓ビラ問題] x,y∈ℂとする. 正の整数nに対し m_n = x^n - y^n p_n = x^n + y^n とおく. (1) x≠yとする. すべてのnでm_nが整数であるならば, x,yはともに整数であることを証明せよ. (2) すべてのnでp_nが整数であるような組(x,y)はどのように表せるか.
書いた! 部分積分を参考にして、微分の定義を積分等式の形に緩められる。 弱微分、ソボレフ空間W^{k,p},H^kとは:簡単な例|趣味の大学数学 math-fun.net/20220822/26294/
A one-page proof of the irrationality of pi.

学部の頃講義でもらった演習問題より

Consider the function f(x) = 1 / ( ⌊x⌋ + 1 − {x} ) and the sequence of numbers 0, f(0), −f(0), f(f(0)), −f(f(0)), f(f(f(0))), −f(f(f(0))), ... Congratulations, you've just listed every rational number exactly once!

United States Trends
- 1. Good Monday 24.1K posts
- 2. #ITZY_TUNNELVISION 33.5K posts
- 3. Steelers 53.6K posts
- 4. Rudy Giuliani 13.8K posts
- 5. Mr. 4 4,772 posts
- 6. #MondayMotivation 29.4K posts
- 7. Happy Birthday Marines 3,268 posts
- 8. Resign 115K posts
- 9. Chargers 38.7K posts
- 10. Schumer 236K posts
- 11. #Talus_Labs N/A
- 12. Tomlin 8,433 posts
- 13. 8 Democrats 10.7K posts
- 14. Happy 250th 1,422 posts
- 15. Aaron Rodgers 10.2K posts
- 16. Tim Kaine 23.5K posts
- 17. Sonix 1,462 posts
- 18. Voltaire 9,443 posts
- 19. Angus King 19.4K posts
- 20. #BoltUp 3,143 posts
Something went wrong.
Something went wrong.